[!NOTE] 参考说明

本笔记参考《深度学习入门：基于Python的理论和实现》（斋藤康毅 著）

感知机是神经网络（深度学习）的起源算法。理解感知机的构造是通向神经网络和深度学习的重要基石。

一. 感知机的基本结构

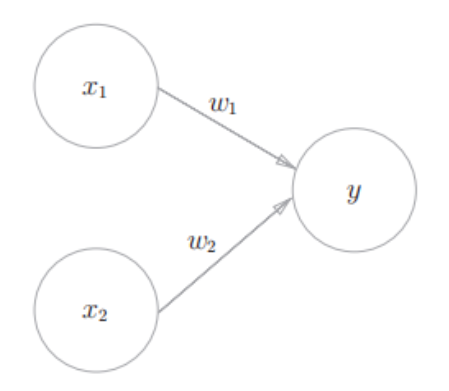
感知机接收多个输入信号，输出一个信号（0 或 1）。

组成要素

  • 输入层：输入数据 。
  • 权重 (Weights)：。权重控制输入信号的重要性，权重越大，对应的输入信号越重要。
  • 偏置 (Bias)：。调整决策边界的偏移量，决定了神经元被激活（输出 1）的难易程度。

数学表达
感知机的计算公式如下：

二. 简单逻辑电路的实现

感知机可以通过设置不同的权重和偏置来实现基本的逻辑门电路。

为了方便复用，我们先定义一个通用的感知机函数，然后再通过传参实现不同的门：

import numpy as np

def perceptron(x1, x2, w1, w2, b):
    x = np.array([x1, x2])
    w = np.array([w1, w2])
    tmp = np.sum(w * x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

1) AND 门（与门）

规则：仅当两个输入均为 1 时，输出 1。

x1​ x2​ y
0 0 0
0 1 0
1 0 0
1 1 1

参数选择：
(解释：只有当 时才输出 1)

def AND(x1, x2):
    return perceptron(x1, x2, 0.5, 0.5, -0.7)

2) NAND 门（与非门）

规则：与 AND 门相反，仅当两个输入均为 1 时，输出 0；其余情况输出 1。

x1​ x2​ y
0 0 1
0 1 1
1 0 1
1 1 0

参数选择：
(解释：权重取负，偏置取正，即可翻转 AND 的逻辑)

def NAND(x1, x2):
    return perceptron(x1, x2, -0.5, -0.5, 0.7)

3) OR 门（或门）

规则：只要有一个输入为 1，输出即为 1。

x1​ x2​ y
0 0 0
0 1 1
1 0 1
1 1 1

参数选择：
(解释：只要有一个 1，结果为 )

def OR(x1, x2):
    return perceptron(x1, x2, 0.5, 0.5, -0.2)

三. 感知机的局限性

虽然感知机可以实现 AND、NAND、OR，但它无法直接实现 异或门 (XOR Gate)。

XOR 问题
规则：仅当 和 不同时，输出 1。

x1​ x2​ y
0 0 0
0 1 1
1 0 1
1 1 0

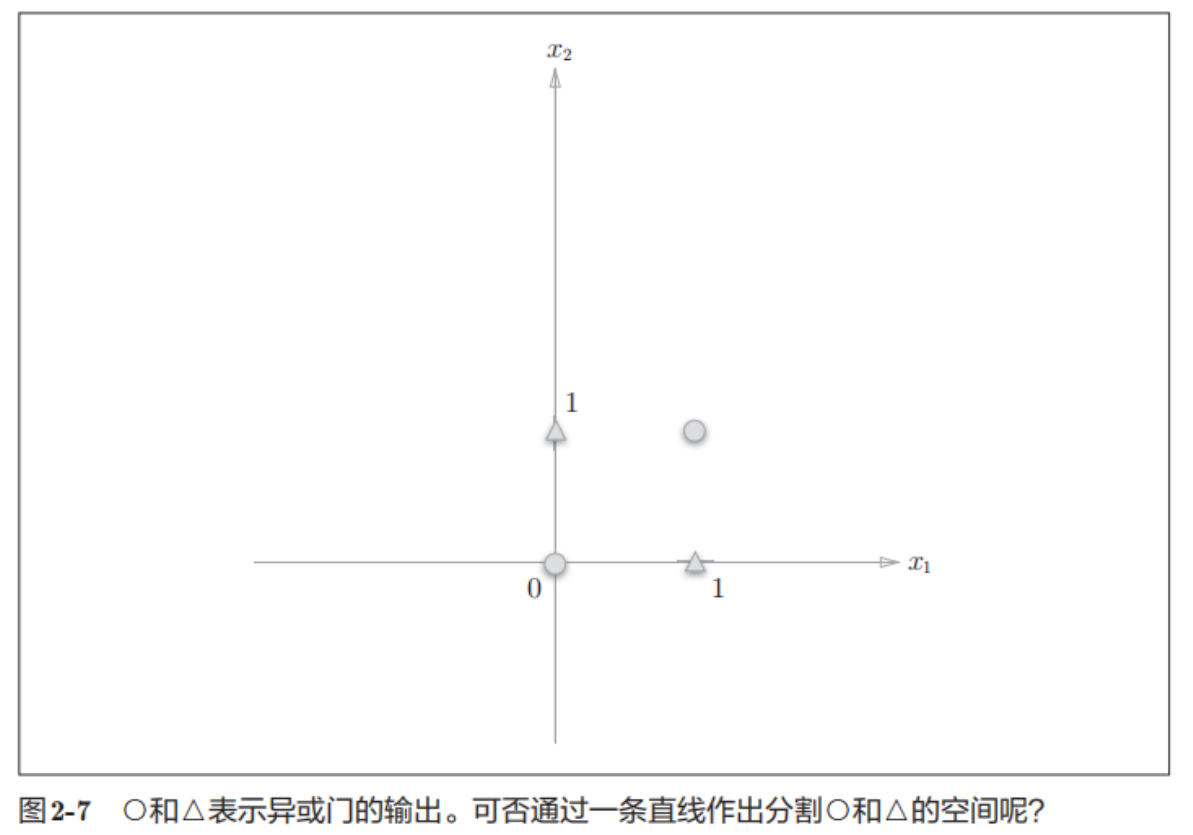
几何解释

  • 线性空间：单层感知机的决策边界是一条直线 ()。
  • 非线性空间：XOR 的数据分布（和是0类，和是1类）无法用一条直线分开。

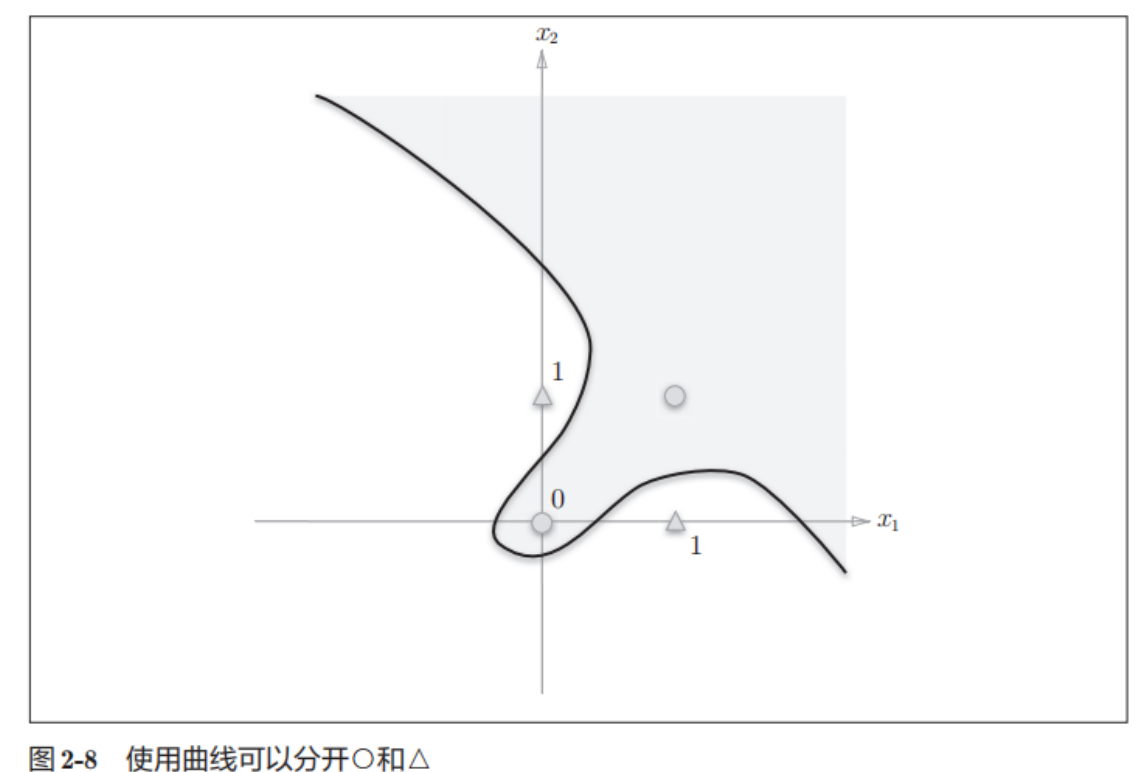
结论：单层感知机无法解决非线性可分问题（如 XOR 问题）。

四. 多层感知机 (Multi-Layer Perceptron, MLP)

感知机的绝妙之处在于它可以“叠加”。虽然单层无法解决 XOR，但我们可以通过组合已有的门电路来实现。

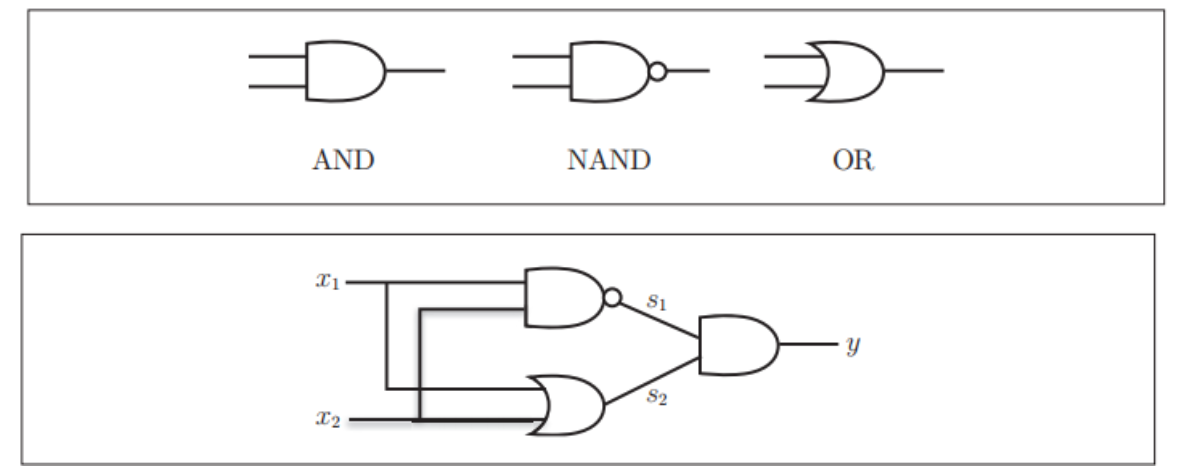
XOR 的组合逻辑：
我们可以用 NAND、OR 和 AND 门组合出 XOR：

  1. NAND 门处理：当输入不全是 1 时为 1。
  2. OR 门处理：当输入至少有一个 1 时为 1。
  3. AND 门汇合：结合上述两个结果。
x1​ x2​ s1​ (NAND) s2​ (OR) y (AND of s1​,s2​) 符合 XOR?
0 0 1 0 0 ✅
1 0 1 1 1 ✅
0 1 1 1 1 ✅
1 1 0 1 0 ✅

代码实现：

def XOR(x1, x2):
    s1 = NAND(x1, x2)  # 第0层到第1层
    s2 = OR(x1, x2)    # 第0层到第1层
    y = AND(s1, s2)    # 第1层到第2层
    return y

# 测试 XOR
print(f"XOR(0, 0) = {XOR(0, 0)}") # 应输出 0
print(f"XOR(1, 0) = {XOR(1, 0)}") # 应输出 1
print(f"XOR(0, 1) = {XOR(0, 1)}") # 应输出 1
print(f"XOR(1, 1) = {XOR(1, 1)}") # 应输出 0

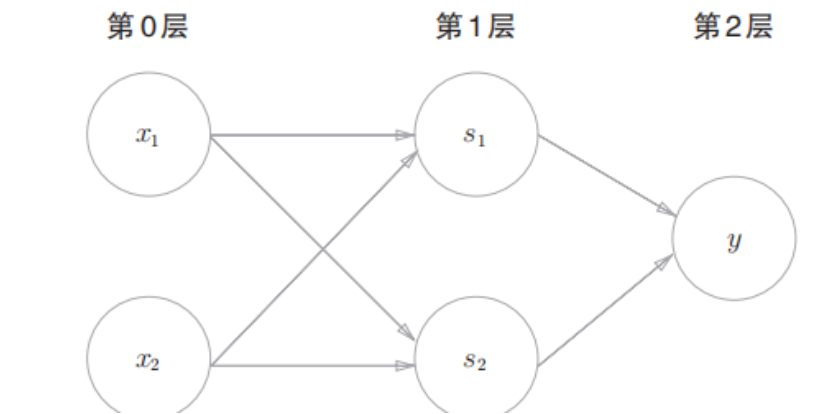
结构图示：

XOR 是一种两层感知机（部分文献根据权重层数称为2层，部分根据神经元层数称为3层，这里指有1个隐藏层）：

  • 第0层：输入
  • 第1层：中间神经元 (NAND, OR)
  • 第2层：输出神经元 (AND)