人工智能基础2-神经网络

[!NOTE] 参考说明

本笔记参考《深度学习入门：基于Python的理论和实现》

一.核心概念对比

感知机

• 优点： 理论上，感知机有潜力表示复杂的函数（计算机的本质就是复杂的逻辑门组合）。
• 缺点： 无法自动学习。确定合适的权重和偏置仍需人工完成（例如手动设计 AND/OR 门的参数）。

神经网络

• 目的： 解决感知机需要人工设定参数的问题。
• 核心性质： 能够自动地从数据中学习到合适的权重参数。

二. 从感知机到神经网络

2.1 神经网络的结构

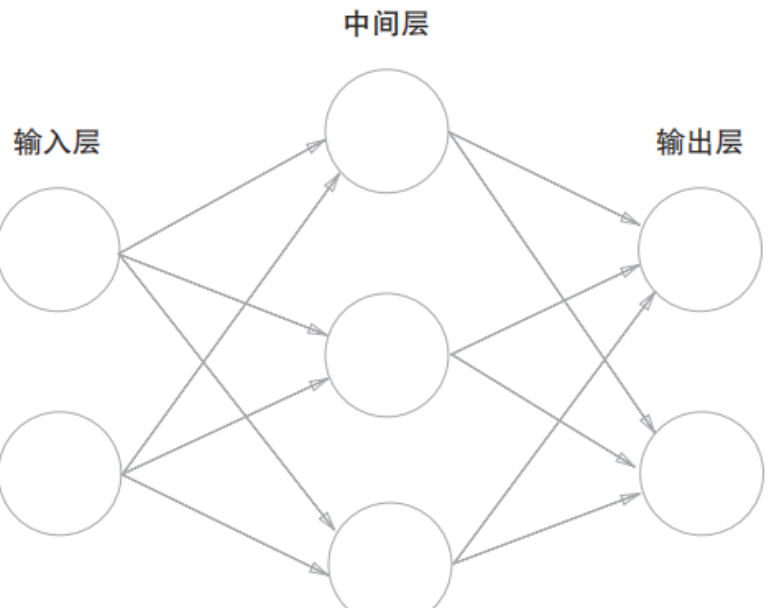
典型的神经网络结构如下图所示：

层级划分：

• 输入层（第 0 层）：接收原始数据。
• 中间层（第 1 层）：也称为隐藏层，因为其神经元在输入和输出之间，肉眼不可见。
• 输出层（第 2 层）：输出最终结果。

[!TIP] 关于层数的命名

图中有 3 列神经元，但通常称为 “2层网络” 或 “3层网络”。

• 本书约定：根据实质上拥有权重的层数（即箭头连接的层数）来命名。输入层到隐藏层（1组权重），隐藏层到输出层（1组权重），故称为 2层网络。

• 也有文献算上输入层称为3层网络。为了避免歧义，通常直接指明“拥有1个隐藏层”。

2.2 数学表达的转换

感知机的数学表达式：

$$y = \begin{cases} 1, & (b + w_1x_1 + w_2x_2 \geq 0) \\ 0, & (b + w_1x_1 + w_2x_2 < 0) \end{cases}$$

在神经网络中，我们将上述公式改写为两步：

1. 计算加权信号的总和：
2. 使用函数 转换总和：

这里引入的 就是 激活函数。

三. 激活函数

3.1 定义与作用

• 定义：将输入信号的总和转换为输出信号的函数。
• 作用：决定如何激活神经元（例如：输入达到多少才输出1，或者是输出一个连续的强度值）。
• 关键区别：
  • 感知机：使用阶跃函数（Step Function）。
  • 神经网络：使用Sigmoid、ReLU 等平滑变化的函数。

3.2 为什么必须是非线性函数？

[!WARNING] 线性函数的陷阱

神经网络的激活函数 必须 使用非线性函数。

原因：如果使用线性函数（如 ），无论网络加深多少层，其本质仍然等同于单层线性变换。

• 例如：3层网络 ，如果 ，则 ，这依然只是一个乘以常数的线性变换。

• 为了发挥多层网络的优势，必须引入非线性因素。

3.3 常见激活函数

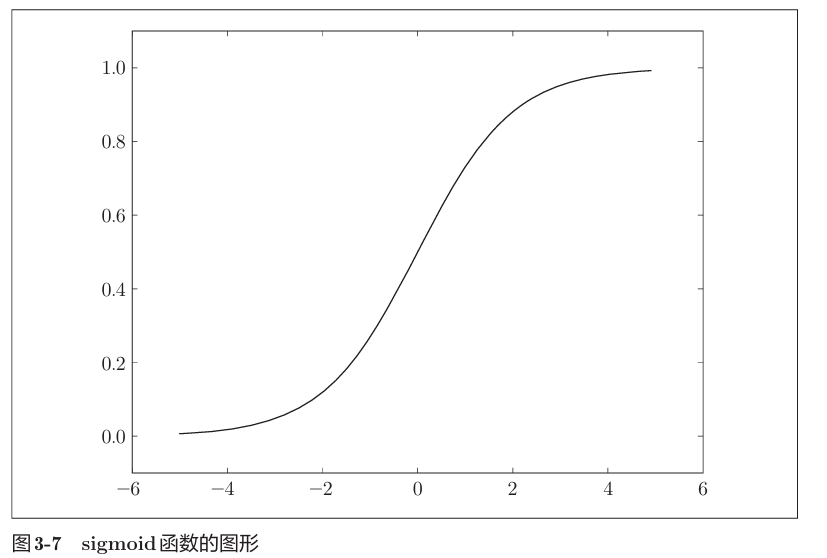
1) Sigmoid 函数

历史上最早被广泛使用的激活函数。

$$h(x) = \frac{1}{1 + e^{-x}}$$

• 输出范围：
• 特点：平滑曲线，输出随输入连续变化。
  

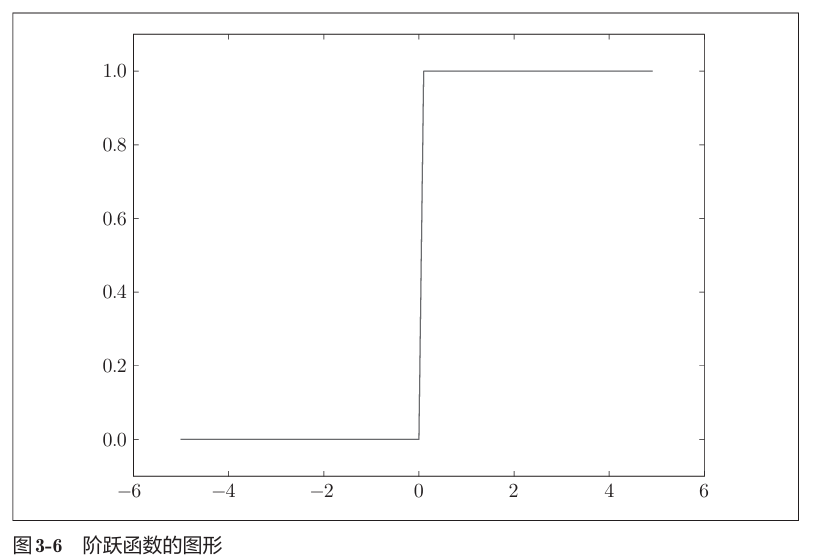
2) 阶跃函数 (Step Function)

感知机使用的函数。

$$h(x) = \begin{cases} 1, & x \geq 0 \\ 0, & x < 0 \end{cases}$$

• 输出范围：
• 特点：在 0 处发生剧烈跳变。
  

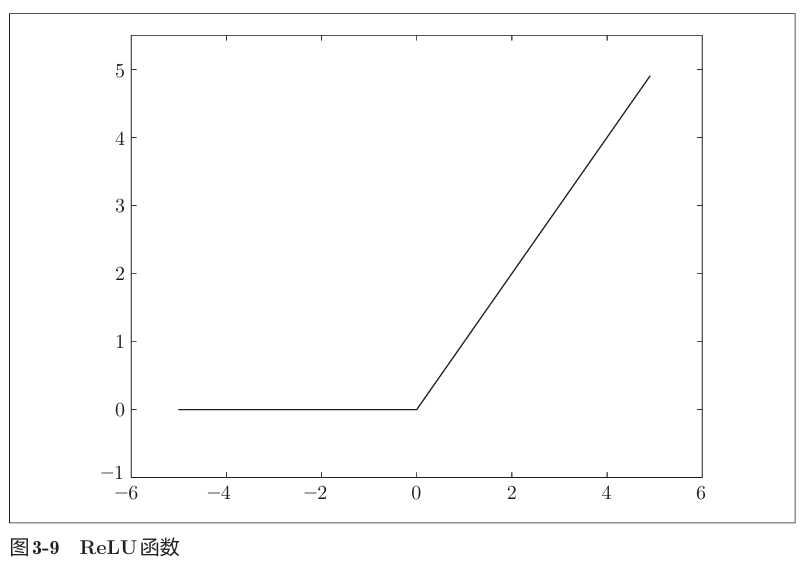
3) ReLU (Rectified Linear Unit)

现代深度学习中最常用的函数。

$$h(x) = \begin{cases} x, & x > 0 \\ 0, & x \leq 0 \end{cases}$$

• 输出范围：
• 特点：输入大于0时直接输出，小于等于0时输出0。计算简单高效。
  

四. 输出层的设计

输出层的激活函数 取决于要解决的问题类型：

问题类型	描述	输出层激活函数
回归问题	预测连续数值 (如预测房价、体重)	恒等函数 (Identity)
分类问题	预测类别 (如识别数字、图像分类)	Softmax 函数

4.1 恒等函数

输入是什么，输出就是什么。

4.2 Softmax 函数 (分类问题)

1. 公式

用于将 个输出转换为概率分布，所有输出之和为 1。

$$y_k = \frac{e^{a_k}}{\sum_{i=1}^{n} e^{a_i}}$$

符号说明：

• ：输出层第 个神经元的输出（即属于第 类的概率）。
• ：输入信号（第 个神经元的加权和，即 Softmax 处理前的值）。
• ：输出层神经元的总个数（即分类的总类别数）。
• ：自然常数（约等于 2.71828…），这里指指数函数 。
• ：归一化常数（分母），即所有输入信号的指数之和。它确保了所有 加起来等于 1。

2. 实现难点：溢出问题

指数函数 增长极快（例如 约为 22026，而 会返回无穷大 inf）。为了防止计算机计算溢出，需要进行改进：

$$y_k = \frac{e^{a_k - C}}{\sum_{i=1}^{n} e^{a_i - C}}$$

符号说明：

• ：用于防止溢出的常数。为了数值稳定性，通常取输入信号中的最大值，即 。
• 原理：在指数函数中减去常数 （相当于分子分母同时除以 ），不会改变最终计算结果 的值，但能将指数运算的范围限制在较小的负数到 0 之间，从而避免溢出。

3. 特性与注意

• 概率性质：输出总和为 1.0 ()。因此 可以被解释为“概率”（例如：图片是猫的概率是 0.8，是狗的概率是 0.2）。
• 单调性：因为指数函数 是单调递增函数，所以 Softmax 处理前后，各元素之间的大小关系（谁大谁小）保持不变。
• 推理阶段可省略：
  • 在实际应用的推理（预测）阶段，因为只需要找出最大值代表的类别，而 Softmax 不改变最大值的位置，所以为了节省计算资源，通常会省略 Softmax 函数。
  • 在神经网络的学习（训练）阶段，为了计算损失函数（Loss），Softmax 函数是必须的。

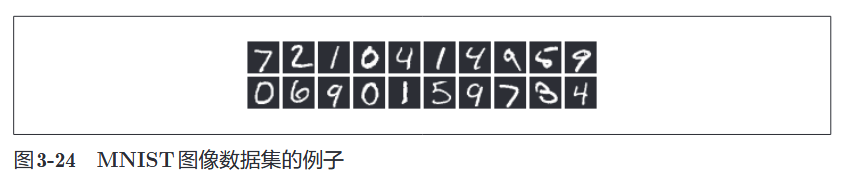
五. 手写数字识别 (MNIST)

为了验证神经网络的效果，我们使用著名的 MNIST 数据集 进行手写数字识别。这是一个经典的机器学习“Hello World”任务。

1) 数据集概况

• 内容：0 到 9 的手写数字图像。
• 数量：训练图像 60,000 张，测试图像 10,000 张。
• 格式：28 x 28 像素的灰度图像（单通道），每个像素值为 0~255。
• 输入数据：为了输入神经网络，我们将 28x28 的图像展平为长度为 784 的一维数组（）。
  

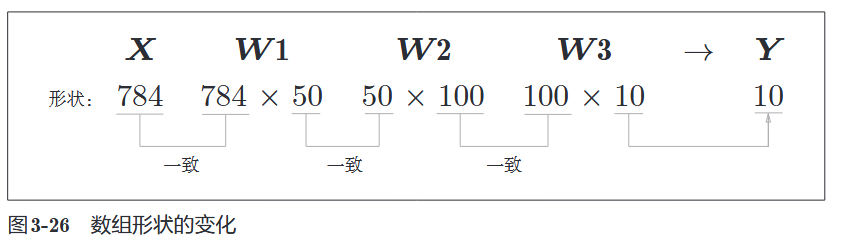
2) 神经网络结构

在这个实战中，我们使用一个包含 2 个隐藏层的神经网络：

• 输入层：784 个神经元（对应图像像素）。
• 隐藏层 1：50 个神经元（人为设定）。
• 隐藏层 2：100 个神经元（人为设定）。
• 输出层：10 个神经元（对应数字 0-9 的分类）。

3) 预处理

为了提高识别精度和训练效率，我们通常对输入数据进行处理。

• 正规化：将像素值从 0~255 除以 255，使其范围变为 0.0~1.0。
• 白化：将数据分布转化为均值为0、方差为1的分布（本例暂不涉及，属于进阶处理）。

4) 推理代码示例

假设我们已经有了训练好的权重参数（保存在 sample_weight.pkl 中），推理过程如下：

import sys, os
import numpy as np
import pickle # 用于读取二进制文件（这里用于读取保存好的权重参数）
from dataset.mnist import load_mnist # 导入书中提供的读取MNIST数据集的函数
from common.functions import sigmoid, softmax # 导入激活函数

def get_data():
    """
    函数功能：获取测试数据
    """
    # load_mnist 是书中自定义的函数，用于下载和加载数据
    # normalize=True:  将图像像素值从 0~255 除以 255，缩放到 0.0~1.0 之间。
    #                  这叫“正规化”，有助于神经网络计算。
    # flatten=True:    将 28x28 的二维图像数组“展平”为长度为 784 的一维数组。
    #                  因为我们的输入层有 784 个神经元。
    # one_hot_label=False: 返回标签为数字本身（比如 7），而不是 One-Hot 编码（比如 [0,0,0,0,0,0,0,1,0,0]）。
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    
    # 因为我们现在是做“推理”（测试），不需要训练数据，所以只返回测试用的图像(x_test)和标签(t_test)
    return x_test, t_test

def init_network():
    """
    函数功能：初始化网络，即加载预先训练好的权重参数
    """
    # sample_weight.pkl 是一个二进制文件，里面保存了已经训练好的权重(W)和偏置(b)
    # 这个文件就像是神经网络“学到的知识”
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f) # 使用 pickle 库加载字典类型的参数
    return network

def predict(network, x):
    """
    函数功能：前向传播（推理过程）
    参数 network: 包含权重和偏置的字典
    参数 x: 输入的一张图像数据（长度为784的数组）
    """
    # 1. 从字典中提取各层的权重(W)和偏置(b)
    # W1, W2, W3 是权重矩阵
    # b1, b2, b3 是偏置数组
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # 2. 第1层运算（输入层 -> 第1隐藏层）
    # np.dot 是矩阵乘法（点积），将输入信号 x 与权重 W1 相乘
    # 加上偏置 b1 后，经过 sigmoid 激活函数处理
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1) 

    # 3. 第2层运算（第1隐藏层 -> 第2隐藏层）
    # 使用上一层的输出 z1 作为输入
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)

    # 4. 第3层运算（第2隐藏层 -> 输出层）
    # 也就是最后一层，输出结果
    a3 = np.dot(z2, W3) + b3
    
    # 5. 输出层处理
    # 使用 softmax 函数将输出转化为概率分布（例如：是0的概率是多少，是1的概率是多少...）
    y = softmax(a3)
    
    return y

# --- 主程序开始 ---

# 1. 获取测试数据
# x 是图像数据，t 是对应的正确标签（Truth）
x, t = get_data()

# 2. 初始化网络（加载权重）
network = init_network()

accuracy_cnt = 0 # 用于记录预测正确的次数

# 3. 循环处理每一张图片
# len(x) 是测试图片的数量（通常是 10000 张）
for i in range(len(x)):
    
    # 对第 i 张图片进行推理，得到预测结果 y
    # y 是一个包含 10 个概率值的数组，例如 [0.01, 0.0, 0.9, ...]
    y = predict(network, x[i])
    
    # np.argmax(y) 获取 y 数组中数值最大的元素的索引
    # 比如 y 中第 7 个元素概率最高，p 就等于 7。这代表模型认为这张图是 7。
    p = np.argmax(y) 
    
    # 将模型的预测结果 p 与 真实标签 t[i] 进行对比
    if p == t[i]:
        accuracy_cnt += 1 # 如果预测正确，计数器加 1

# 4. 计算并打印准确率
# 准确率 = 预测正确的次数 / 总图片数
# float() 是为了执行浮点数除法，保留小数
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

六. 批处理

1) 批处理相关知识

在上面的代码中，我们是用 for 循环一张一张处理图片的。

• 问题：处理速度慢，无法充分利用数值计算库（NumPy）对大型数组运算的优化。
• 解决：一次性打包处理多张图片（例如 100 张），这个“包”称为 Batch。

1.概念与定义

• 定义：这种打包式输入的输入数据称为批 (Batch)。
• 形象理解：如果把单张图像数据比作一张纸币，批处理就像是把纸币扎成一捆来进行处理。

2.核心优势

• 速度提升：批处理对计算机运算非常有百利而无一害，可以大幅缩短每张图像的处理时间。

3.原理：为什么批处理更快？
批处理之所以能加速，主要归功于以下两点计算机底层机制：

1. 数值计算库的优化： 大多数处理数值计算的库（如 NumPy）都针对大型数组运算进行了专门的最优化。一次计算一个大的矩阵，比分多次计算小的矩阵效率更高。
2. 缓解数据传输瓶颈： 在神经网络运算中，数据的传输（读取）往往是瓶颈。
   • 减轻总线负荷：批处理可以减轻数据总线的负荷。
   • 提高计算占比：严格来说，批处理让计算机减少了花在“读入数据”上的比例，将更多的时间用在纯粹的“计算”上。

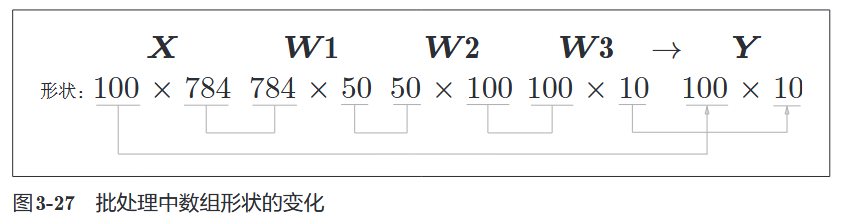
2) 形状的变化

假设 Batch Size 为 100：

• 输入 X：从 (784,) 变为 (100, 784)。
• 输出 Y：从 (10,) 变为 (100, 10)。
  
  

3) 批处理代码实现

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    
    # axis=1 表示在第1维（行方向）上寻找最大值的索引
    p = np.argmax(y_batch, axis=1)
    
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))