人工智能基础4-误差反向传播法

[!NOTE] 参考说明

本笔记参考《深度学习入门：基于Python的理论和实现》

神经网络梯度计算：
数值微分：实现简单，但计算量大，速度慢（上一章的方法）。
误差反向传播法：实现稍复杂，但计算速度极快，是训练深度神经网络的必经之路。

一. 计算图

为了直观地理解误差反向传播，书中引入了计算图的概念。

1.1 什么是计算图？

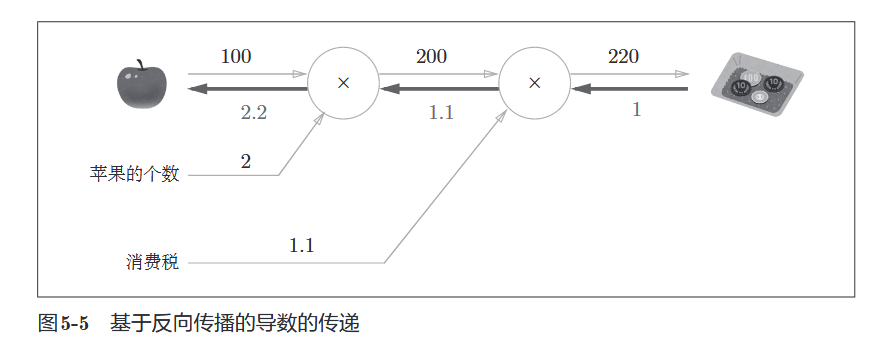
将计算过程用“节点”和“箭头”表示的图形。

正向传播 (Forward)：从左向右。计算结果（例如：买了多少钱）。
反向传播 (Backward)：从右向左。计算导数（例如：苹果价格波动 1 元，总价波动多少）。

1.2 局部计算

定义：每个节点只关注自己相关的两个输入和输出，不用管全局。
【直观理解】：
- 比如你在收银台结账（最后的节点）。你只需要把“单价数量”算好传给下一个环节（加税）。你不需要知道这个苹果是哪里摘的，也不需要知道税率是多少。
- 意义：这让我们可以把极其复杂的神经网络，拆解成无数个简单的“加法”和“乘法”积木。

1.3 为什么用计算图？

局部计算：简化问题，无论多复杂的网络都能分解成简单的节点。
保存中间结果：正向传播时的中间值可以被保存，供反向传播使用。
反向传播高效计算导数：这是最重要的理由。

二. 链式法则

反向传播的数学原理是链式法则。

2.1 定义

如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。

假设，，求：

$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \cdot \frac{\partial t}{\partial x}$

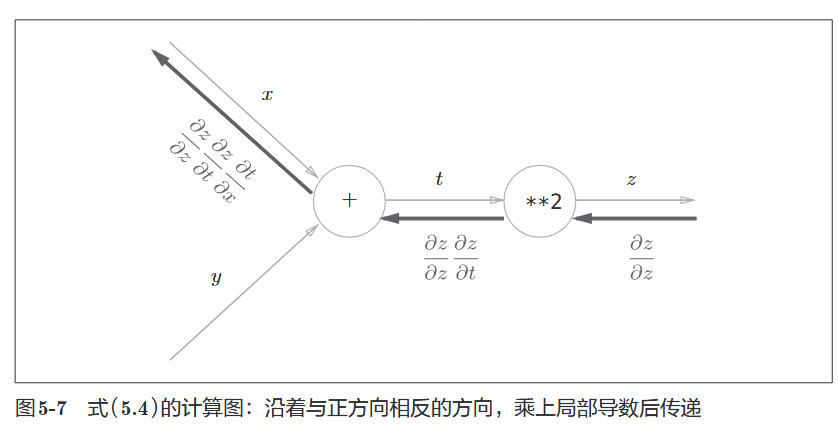
2.2 计算图中的链式法则

反向传播将上游传来的导数（对该节点输出的导数）乘以当前节点的局部导数，然后传给下游。
公式： $下游导数上游导数局部导数$

三. 简单层的实现

3.1 加法层

正向：
导数：

反向传播：将上游传来的导数原封不动地传给下游（乘以 1）。

class AddLayer:
    def __init__(self):
        pass
    def forward(self, x, y):
        return x + y
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1
        return dx, dy

3.2 乘法层

正向：
导数：

反向传播：将上游传来的导数乘以正向传播时的“翻转值”。

传给的导数是

传给

的导数是

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
        
    def forward(self, x, y):
        self.x = x # 必须保存输入，反向传播要用
        self.y = y
        return x * y
        
    def backward(self, dout):
        dx = dout * self.y # 翻转 x -> 乘 y
        dy = dout * self.x # 翻转 y -> 乘 x
        return dx, dy

五. 激活函数层的实现

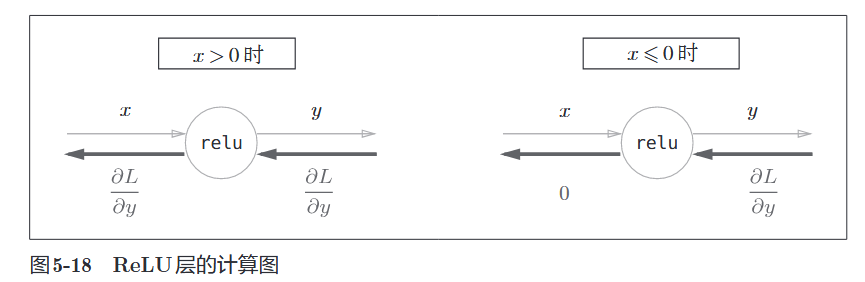
4.1 ReLU 层

公式：

$y = \begin{cases} x & (x > 0) \\ 0 & (x \leq 0) \end{cases}$

导数：

$\frac{\partial y}{\partial x} = \begin{cases} 1 & (x > 0) \\ 0 & (x \leq 0) \end{cases}$

直观理解：
- 正向传播时，如果水流过了（），反向传播时导数也流过（乘以1）。
- 正向传播时，如果被挡住了（），反向传播时导数也被挡住（变为0）。

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0) # 记录哪些位置小于等于0
        out = x.copy()
        out[self.mask] = 0
        return out

    def backward(self, dout):
        dout[self.mask] = 0 # 小于0的地方导数设为0
        dx = dout
        return dx

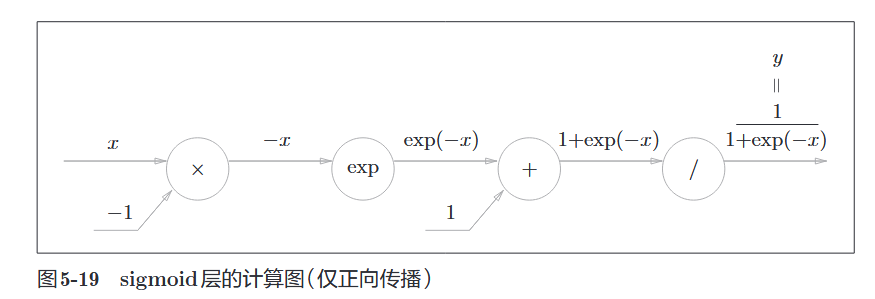
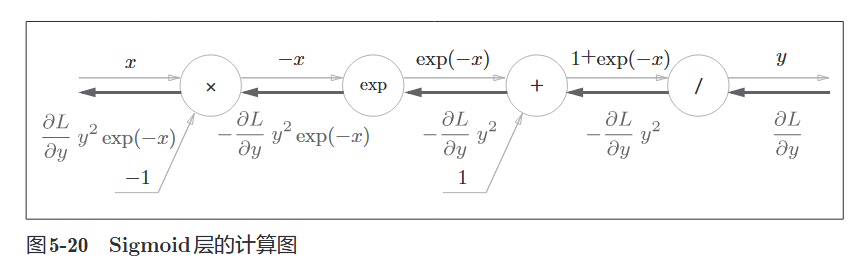
4.2 Sigmoid 层

公式：

经过一系列链式法则推导（, , , ），最终得到的精简导数公式为：

$\frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} \cdot y(1-y)$

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out # 保存输出 y
        return out

    def backward(self, dout):
        # 直接使用公式: dout * y * (1 - y)
        dx = dout * (1.0 - self.out) * self.out
        return dx

五. Affine / Softmax 层

5.1 Affine 层 (矩阵乘积)

神经网络的正向传播主要进行矩阵乘积运算：。

反向传播时，需要利用矩阵转置 () 来匹配形状。

5.2 Softmax-with-Loss 层

组合：为了简化计算，我们将输出层 (Softmax) 和 损失函数 (Cross Entropy) 合并成一层。
【核心解读 - 完美的巧合】：
- 数学推导后，这一层的反向传播结果竟然是：。
- ：你的预测（比如 0.9）。
- ：真实答案（比如 1.0）。
- ：误差（-0.1）。
- 意义：误差本身就是梯度！ 预测越离谱，梯度越大，参数修正得越狠。这是人为设计损失函数时追求的优美性质。。

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        # 注意要除以 batch_size，传递单个数据的平均误差
        dx = (self.y - self.t) / batch_size
        return dx

六. 误差反向传播法的实现

神经网络学习的全貌图：

Mini-batch：随机选取一部分数据。
计算梯度：计算损失函数关于各个权重参数的梯度。
更新参数：将权重沿梯度反方向微调（乘以学习率）。
重复：重复步骤 1-3。

误差的反向传播将在步骤2出现。

具体代码：

def gradient(self, x, t):
        """
        通过误差反向传播法计算梯度
        x: 输入数据
        t: 监督数据
        """
        # 1. 前向传播 (Forward)
        # 必须先运行一次前向传播，让各个层保存中间结果（如 ReLU 的 mask，Affine 的 x）
        self.loss(x, t)

        # 2. 反向传播 (Backward)
        # 初始化上游导数 dout = 1 (因为 dL/dL = 1)
        dout = 1
        
        # 先经过最后一层 (SoftmaxWithLoss)
        dout = self.lastLayer.backward(dout)
        
        # 取出所有层，并反转顺序 (Affine2 -> Relu1 -> Affine1)
        layers = list(self.layers.values())
        layers.reverse()
        
        # 依次调用每个层的 backward 方法，传递导数
        for layer in layers:
            dout = layer.backward(dout)

        # 3. 提取梯度
        # Affine 层在运行 backward() 后，内部已经计算并保存了 dW 和 db
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads

import sys, os
import numpy as np
from dataset.mnist import load_mnist
# 假设上一节定义的包含层(Layer)的 TwoLayerNet 类保存在 two_layer_net.py 中
from two_layer_net import TwoLayerNet 

# 1. 读入数据
# one_hot_label=True：因为我们的 SoftmaxWithLoss 层预期 t 是 one-hot 编码
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

# 初始化网络
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 2. 超参数设定
iters_num = 10000   # 适当设定循环的次数
train_size = x_train.shape[0] # 60000
batch_size = 100    # Mini-batch 大小
learning_rate = 0.1 # 学习率

train_loss_list = []
train_acc_list = []
test_acc_list = []

# 计算 epoch (一轮) 需要的迭代次数 (600次)
iter_per_epoch = max(train_size / batch_size, 1)

print("训练开始... (使用误差反向传播法)")

# 3. 训练循环
for i in range(iters_num):
    # --- 步骤 1: Mini-batch (获取数据) ---
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # --- 步骤 2: 计算梯度 (核心!) ---
    # 使用误差反向传播法求梯度 (高速!)
    # 注意：这里调用的是 gradient() 而不是 numerical_gradient()
    grad = network.gradient(x_batch, t_batch)
    
    # --- 步骤 3: 更新参数 ---
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]
        
    # 记录损失函数值
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    
    # --- 步骤 4: 评价泛化能力 (每个 epoch 打印一次) ---
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(f"Epoch: {int(i/iter_per_epoch)} | Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}")

print("训练结束")