人工智能基础5-与学习相关的技巧

[!NOTE] 参考说明

本笔记参考《深度学习入门：基于Python的理论和实现》

下述内容可简单了解，具体使用时再说。

本章核心
神经网络的学习不仅仅是梯度的计算。为了让模型训练得更好，我们需要关注： 1.参数更新方法（除了 SGD 还有更好的吗？）
2.权重初始值（一开始的参数怎么设？）
3.Batch Normalization（如何强制调整数据分布？）
4.正则化（如何防止过拟合？）
5.超参数最优化（学习率等参数怎么调？）

一. 参数的更新

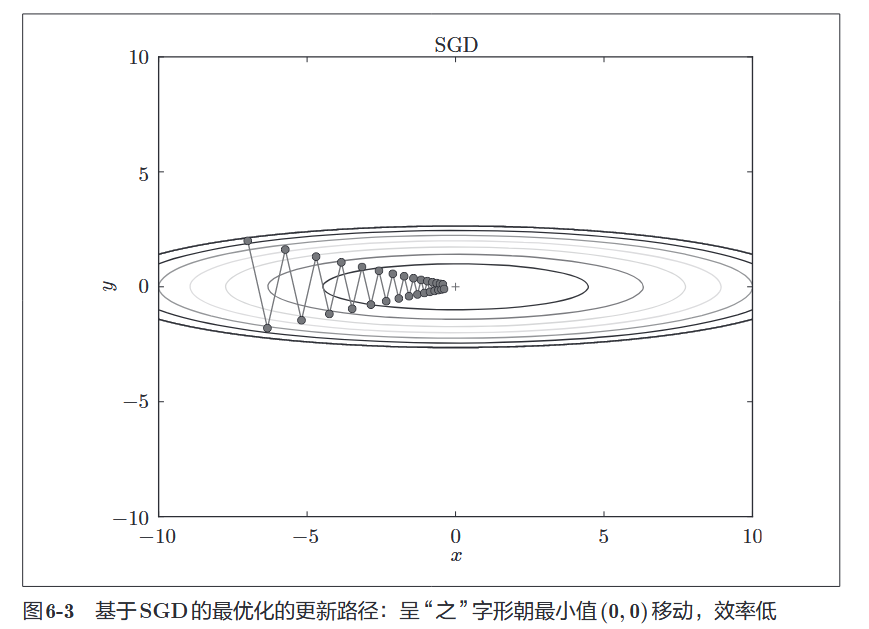
SGD 是最基础、最简单的优化算法。它的核心思想是：朝着梯度方向的反方向，一步一步地更新参数。

我们在前面一直使用的是 SGD (随机梯度下降)。虽然简单，但它在处理某些复杂地形（如延伸状的函数曲面）时效率很低。

1.1 SGD 的缺陷

$W \leftarrow W - \eta \frac{\partial L}{\partial W}$

1. 在“非均向”函数上效率极低

非均向：指的是函数形状在不同方向上延伸程度不同（例如：像一个沿着 x 轴拉长的“碗”或椭圆山谷）。
现象：在这种函数上，梯度的特征是：
- 在陡峭的方向（如 y 轴）梯度很大。
- 在平缓的方向（如 x 轴）梯度很小。
  2. 根本原因：梯度的误导
SGD 单纯地朝着梯度的反方向前进。
但在非均向函数中，梯度的方向大多并没有指向最小值的方向（即），而是指向了山谷的“内壁”。
3. 后果：“之”字形移动
由于上述原因，SGD 会表现出一种极其低效的路径：
- 在坡度大的方向（y 轴）上大幅震荡（过冲）。
- 在坡度小的方向（x 轴）上移动缓慢。
结果就是 SGD 呈“之”字形移动，迟迟无法到达最低点，造成学习效率低下。

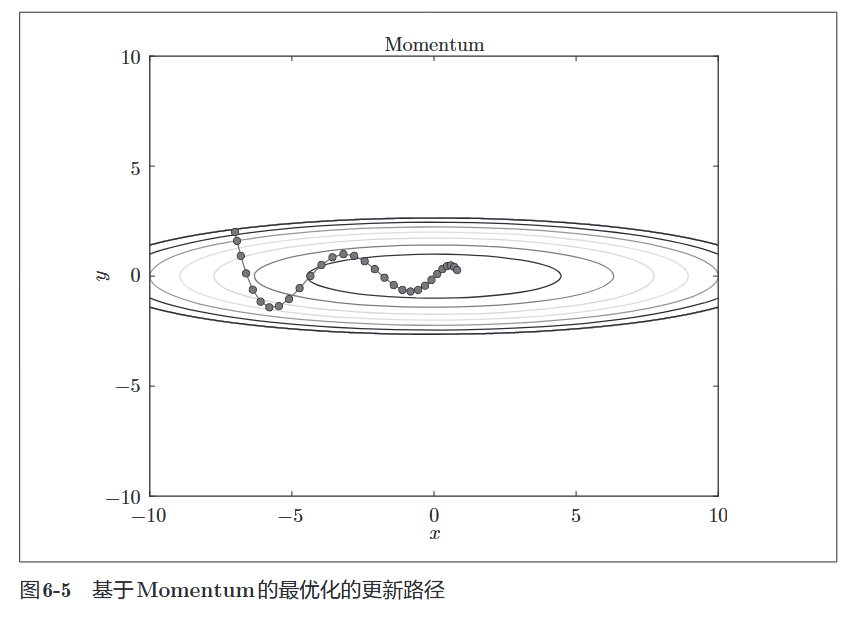
1.2 Momentum (动量)

1. 形象的物理比喻：滚下山的巨石

SGD 就像是一个盲人下山。他每次只摸一下脚下的路，发现哪边陡就往哪边迈一步。他没有记忆，每一步都是新的开始。如果路面是波浪形的，他就会像无头苍蝇一样乱撞（Zigzag 震荡）。
Momentum 就像是一块从山上滚下来的巨石。
- 它有惯性：即使脚下的地形突然变平了，石头因为之前的速度，还会继续向前滚。
- 它有加速度：如果一直在下坡，石头会越滚越快。

2. 公式详解
Momentum 引入了一个新的变量 (Velocity，速度)。

$\begin{aligned} (1) \quad & v \leftarrow \alpha v - \eta \frac{\partial L}{\partial W} \\ (2) \quad & W \leftarrow W + v \end{aligned}$

公式 (1)：计算现在的速度
- ：速度。它不仅仅取决于当前的坡度，还取决于过去的速度。
- ：当前的力（重力）。这是 SGD 里的梯度更新量。它给物体提供新的加速度。
- ：过去的惯性。 (alpha) 是一个 0 到 1 之间的小数（通常取 0.9）。
  - 它的意思是：保留上一时刻 90% 的速度。
  - 这也对应着物理中的“空气阻力”或“摩擦力”。如果没有这项，物体会无限加速；有了这项，物体会慢慢减速。
- 总结：新速度 = (0.9 老速度) + (当前的梯度力)。
公式 (2)：更新位置
- ：现在我们要移动参数了。注意！我们不再是根据梯度移动，而是根据速度来移动。

3. 为什么它能解决 SGD 的问题？
让我们回到那个 SGD 表现很差的“峡谷”地形（Y轴坡度陡，X轴坡度缓）：

在 Y 轴（陡峭方向）：
- 梯度一会儿正，一会儿负（震荡）。
- 因为动量会把过去的速度加起来：。
- 正负相互抵消！惯性抑制了震荡，让它不会在山谷两壁乱撞。
在 X 轴（平缓方向）：
- 梯度虽然小，但方向一直一致（比如一直是 +1）。
- 动量不断累积：速度越来越快。
- 加速收敛：它能更快地冲向谷底。

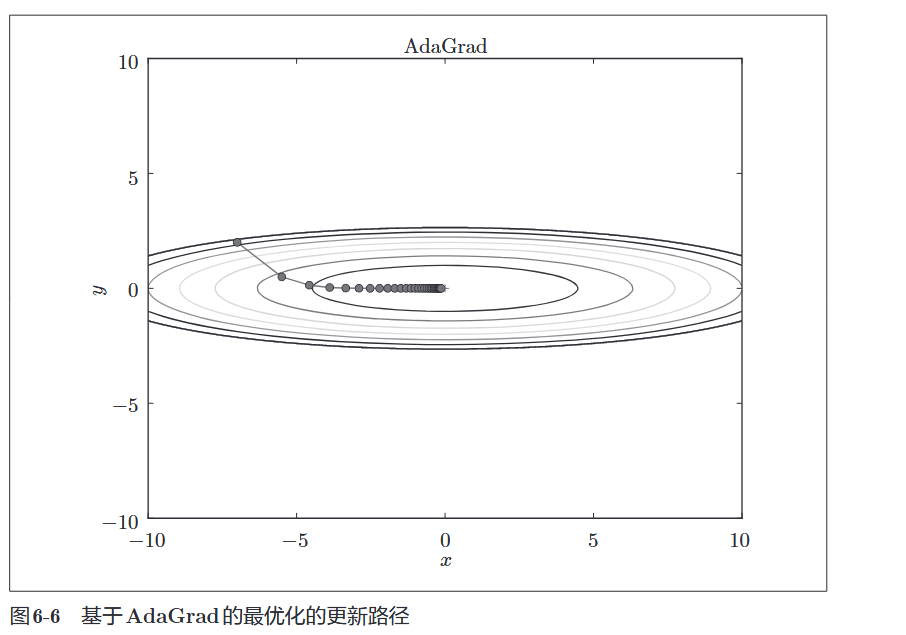
1.3 AdaGrad

核心思想：学习率衰减。

对于更新频繁（梯度大）的参数，给予更小的学习率。
对于更新不频繁（梯度小）的参数，给予更大的学习率。

公式：

$h \leftarrow h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W}$ $W \leftarrow W - \eta \frac{1}{\sqrt{h} + \epsilon} \frac{\partial L}{\partial W}$

公式 (1)：累积梯度的平方
- ：矩阵元素的乘法。即对应位置的元素相乘，不是矩阵乘法。
- ：把梯度的每个元素都平方。
- ：这是一个和权重形状一样的矩阵。它像一个记分牌，记录了从训练开始到现在，每个参数的梯度“能量”的总和。
  - 为什么要平方？ 这样可以去掉负号，只关注梯度的大小（幅度）。
  - 为什么要累加？ 为了知道这个参数在过去的历史中是不是一直变动很剧烈。
公式 (2)：自适应更新
- ：开根号，调整量级。
- ：关键所在！
  - 如果某个参数过去梯度很大（陡峭），就会很大，分母变大，变小 学习率变小（小心翼翼地走）。
  - 如果某个参数过去梯度很小（平坦），就会很小，分母变小，变大 学习率变大（大步流星地走）。
- (epsilon)：一个极小值（如）。防止分母为 0，避免程序报错。

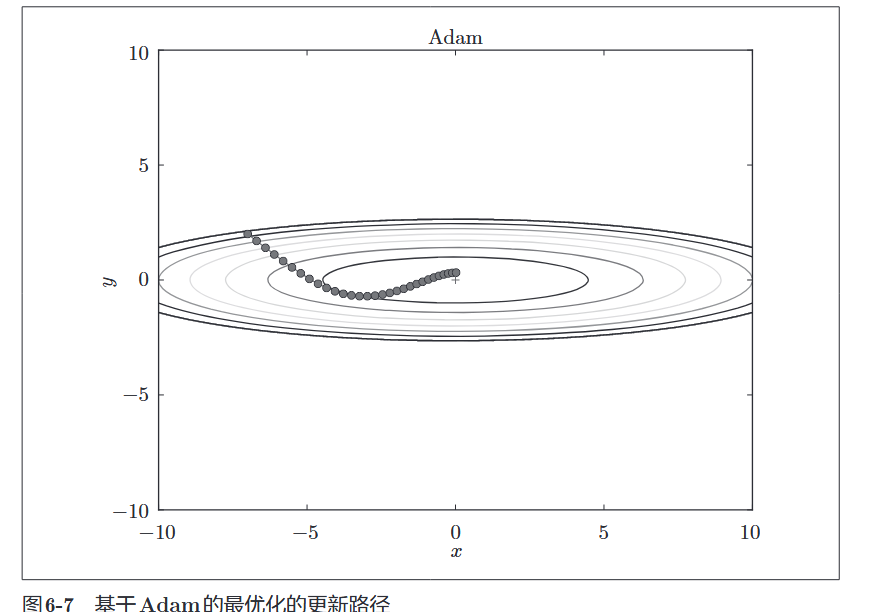
1.4 Adam

核心思想：Momentum + AdaGrad 的结合体。

既利用了动量（惯性）来加速。
又利用了自适应学习率来调整步长。
地位：目前深度学习中最常用的优化器之一。

二.权重的初始值

2.1 可以将权重初始值设为 0 吗？

1.权值衰减的背景
为了抑制过拟合，我们有一种称为权值衰减的技术。

核心思想：过拟合通常伴随着权重参数过大。因此，我们在损失函数中加入惩罚项，强制让权重变小。
推论：既然希望权重变小，那我们一开始就把初始值设得很小（如 0.01 甚至 0），岂不美哉？

2.为什么不能将初始值设为 0？
虽然我们希望权重小，但绝对不能将所有权重初始化为 0（或任何相同的值）。

原因：对称性问题
- 前向传播：如果，所有神经元接收到的输入都相同，输出也完全相同。
- 反向传播：所有权重的梯度也完全相同。
- 结果：无论更新多少次，所有权重的值都保持一致。这使得包含几百个神经元的隐藏层实际上退化成了单个神经元。
必须“破坏对称性”：我们需要随机生成初始值，确保每个神经元能学到不同的特征。

2.2 隐藏层激活值的分布

在神经网络中，隐藏层的输出（即经过激活函数后的值）被称为激活值。
我们希望：各层激活值的分布应该有适当的广度（尽可能均匀）。

1. 为什么要关注激活值分布？

如果激活值分布得不好，会引发两个致命问题，导致网络无法训练：

梯度消失
- 现象：激活值集中在 0 和 1 的两端（针对 Sigmoid 函数）。
- 原因：Sigmoid 函数的图像呈 S 型。当输出接近 0 或 1 时，其导数（斜率）接近于 0。
- 后果：在反向传播时，梯度不断乘以这些接近 0 的导数，导致梯度迅速衰减，底层参数几乎无法更新。
表现力受限
- 现象：激活值集中在 0.5 附近（针对 Sigmoid 函数）。
- 原因：Sigmoid 函数在 0.5 附近近似于线性函数。如果所有神经元的输出都差不多，那么使用多个神经元就失去了意义（100 个输出相同的神经元等价于 1 个神经元）。
- 后果：网络变得太简单，无法拟合复杂的非线性模式。

2. 实验：权重初始值如何影响分布？

假设我们使用 Sigmoid 作为激活函数，观察不同标准差（std）的高斯分布初始化带来的后果：

初始值设定	分布形态 (直方图)	导致的问题	原理解析
标准差很大 `std = 1.0`	两端集中 (0 和 1 附近)	梯度消失	权重过大神经元加权和过大 Sigmoid 饱和导数为 0。
标准差很小 `std = 0.01`	中心集中 (0.5 附近)	表现力受限	权重过小神经元加权和接近 0 Sigmoid 处于线性区无法学习复杂特征。

3. 解决方案：使用专业的初始化方法

为了让激活值分布既不靠边也不扎堆，学者们提出了专门的初始化标准：

Xavier 初始值
- 适用场景：激活函数是 Sigmoid 或 Tanh（S 型曲线）。
- 公式：标准差设为（为前一层的节点数）。
- 效果：前一层节点越多，初始权重越小，保持输出方差一致，激活值分布均匀。
He 初始值
- 适用场景：激活函数是 ReLU。
- 公式：标准差设为。
- 原理：因为 ReLU 会将负值置为 0（砍掉一半信号），为了保持方差，权重需要比 Xavier 大倍。

三. Batch Normalization (批归一化)

核心痛点：
在神经网络训练中，随着参数不断更新，各层数据的分布会不断发生变化。这迫使每一层都要不断适应新的分布，导致训练变慢，且对初始值非常敏感。

核心思路：
强制性调整。既然数据分布容易乱，不如在每一层（通常是激活函数之前）强制把输入数据调整为标准正态分布（均值为 0，方差为 1）。

3.1 算法流程

Batch Norm 通常插入在全连接层/卷积层之后，激活函数之前。

$\text{Affine} \rightarrow \text{Batch Norm} \rightarrow \text{ReLU}$

以一个 Mini-batch ( 个数据) 为单位：
第一步：计算统计量 计算当前批次数据的均值和方差。
第二步：归一化 (Normalization) 将数据转换为均值为 0、方差为 1 的分布。

$\hat{x}_i \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$

(epsilon)：一个微小值（如），防止分母为 0。

第三步：缩放和平移 这是 Batch Norm 的精髓。单纯的归一化可能会破坏数据原本的特征。因此，引入两个可学习的参数和进行变换：

$y_i \leftarrow \gamma \hat{x}_i + \beta$

(缩放因子)：控制分布的宽窄。
(平移因子)：控制分布的中心位置。
作用：让网络自己学习是否需要保留归一化，或者“还原”回原来的分布。如果，则等同于只做归一化。

3.2 优点

学习速度快：解决了梯度消失/爆炸问题，可以使用更大的学习率。
不依赖初始值：对权重初始值的依赖大大降低（不用那么小心翼翼地选 Xavier 或 He 了）。
抑制过拟合：
- 因为均值和方差是基于 Mini-batch 计算的，不同的 Batch 会带来随机噪声。
- 这种噪声像 Dropout 一样，迫使网络不过度依赖特定的神经元，具有轻微的正则化效果。

四. 正则化 (Regularization)

问题定义：过拟合 模型“死记硬背”了训练数据，导致泛化能力差。

表现：训练集精度极高（如 99%），测试集精度惨淡（如 80%）。
主要原因：
1. 参数过多：模型太复杂，表现力过剩。
2. 数据太少：样本不足以反映真实分布。

4.1 权值衰减

1. 核心思想

惩罚大权重：过拟合的模型往往伴随着很大的权重参数（曲线剧烈波动）。
策略：在损失函数中增加一个“惩罚项”，如果权重变大，损失函数的值也会剧增。迫使模型在学习时倾向于选择较小的权重。

2.数学实现 (L2 范数)
我们在原有的损失函数上加上权重的平方和（L2 范数）。

$L_{new} = L_{old} + \frac{1}{2} \lambda \sum W^2$

：控制正则化强度的超参数。越大，对大权重的惩罚越重。
的作用：纯粹是为了求导方便。因为求导是，乘以刚好抵消，结果变成。

3.对梯度的影响 (反向传播)
求导后，权重的梯度变为：

$\frac{\partial L_{new}}{\partial W} = \frac{\partial L_{old}}{\partial W} + \boldsymbol{\lambda W}$

在更新参数时：

$W \leftarrow W - \eta (\frac{\partial L_{old}}{\partial W} + \lambda W)$ $W \leftarrow \mathbf{(1 - \eta \lambda)W} - \eta \frac{\partial L_{old}}{\partial W}$

解读：每次更新时，权重都会先乘以一个小于 1 的系数，这就是“衰减”的物理含义——权重会不断地向 0 收缩。

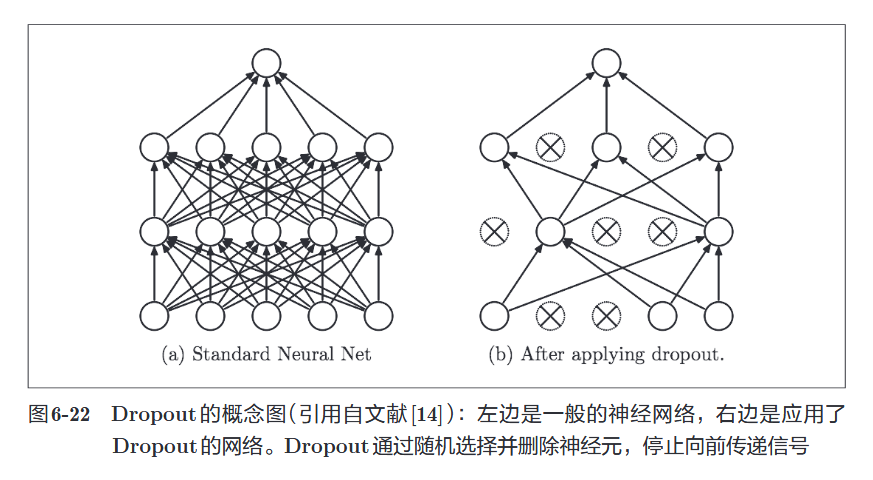
4.2 Dropout

当网络变得极其复杂（深度学习）时，简单的权值衰减可能不够用，这时需要 Dropout。

1.核心思想
在训练过程中，随机删除（临时失活）一部分神经元，打断神经元之间的协同适应。

2. 运作过程

训练时 (Training)：
- 每传递一批数据（Mini-batch），随机选择一部分神经元（比如 50%），将其输出强制设为 0。
- 相当于每次都在训练一个“残缺”的、结构不同的神经网络。
测试时 (Testing)：
- 所有神经元都激活（不删除）。
- 数值调整：为了保证输出信号的总能量与训练时保持一致，需要将神经元的输出乘以删除比例 $'_' allowed only in math mode(1 - \text{dropout_ratio})$ 。

五. 超参数最优化

超参数：无法由网络自动学习，需人工设定的参数（学习率、Batch Size、权重衰减系数、层数等）。

5.1 数据划分

重要原则：千万不能用测试数据 (Test Data) 来调整超参数
如果用测试数据调整，模型就会对测试数据过拟合，失去泛化能力的评价标准。
数据切分：

训练数据 (Train)：用于参数（权重、偏置）的学习。
验证数据 (Val)：用于超参数的评估和调整。
测试数据 (Test)：只在最后用一次，检查泛化能力。

5.2 寻找策略

超参数的搜索不像权重更新那样有梯度指引，通常采用试错法。

设定范围：大致规定一个范围（通常是 10 的对数尺度，如到）。
随机采样：在范围内随机取值。
- _注意_：随机搜索通常比网格搜索效果好，因为超参数的重要性不同。
缩小范围：观察结果，缩小范围，重复搜索（由粗到精）。