二叉树

一、基本概念

二叉树是一种特殊的树结构，其中每个节点最多只有两个子节点，分别称为左子节点 和 右子节点。

术语	描述
根节点 (Root)	树的起始节点，没有父节点。
叶子节点 (Leaf)	没有子节点的节点。
度 (Degree)	节点拥有的子树数量（在二叉树中度最大为 2）。
深度/高度 (Depth/Height)	从根节点到最远叶子节点的最长路径上的节点数（或边数）。

二、特殊类型的二叉树

1. 满二叉树

• 定义： 一棵深度为 且拥有 个节点的二叉树。
• 特性： 树中所有非叶子节点的度都为 2，且所有叶子节点都在同一层（最底层）。
• 判断标准： 节点总数 满足 。

2. 完全二叉树

• 定义： 深度为 ，有 个节点的二叉树。它的节点排列与满二叉树的前 个节点排列完全一致。
• 特性：
  • 只有最底层（第 层）可能不满。
  • 第 层的节点必须从左向右连续排列，中间不能有空缺。
• 用途： 堆 (Heap) 的底层结构就是完全二叉树，因为它允许用数组来高效地存储和访问节点。

三、二叉树的遍历

遍历是指按特定顺序访问树中的每个节点，每个节点仅访问一次。

遍历方式	顺序	递归实现	非递归实现
1. 前序遍历 (Preorder)	根 左 右	易	使用栈
2. 中序遍历 (Inorder)	左 根 右	易	使用栈
3. 后序遍历 (Postorder)	左 右 根	易	使用栈（或两栈）
4. 层次遍历 (Level Order)	从上到下，从左到右	不常用	使用队列

四、二叉搜索树 (Binary Search Tree, BST)

1. 基本概念

• 定义： 一种特殊的二叉树，用于高效查找、插入和删除操作。
• 特性：
  1. 节点 的 左子树 中所有节点的值都小于 的值。
  2. 节点 的 右子树 中所有节点的值都大于 的值。
  3. 左、右子树本身也是二叉搜索树。
• 如果你对一棵 BST 进行中序遍历（左 -> 根 -> 右），得到的结果一定是一个升序排列的序列。

2.当前节点子树的最小节点

• 核心逻辑：根据 BST “左小右大”的性质，子树的最小值一定位于该子树最左侧的末端。只需从当前节点开始，一直向左走直到没有左孩子为止。
• 时间复杂度：
  • 平均情况：。路径长度取决于树的高度。
  • 最坏情况：。如果树是一个向左倾斜的单链表。

    // 1. 查找当前节点子树的最小节点
    Node* findMin(Node* node) {
        if (node == nullptr) return nullptr;
        while (node->left != nullptr) {
            node = node->left;
        }
        return node;
    }

3.查找节点

• 核心逻辑：从根开始，将目标值与当前节点比较。若小则往左走，若大则往右走，相等则命中。
• 时间复杂度：
  • 平均情况：。每次比较都能排除大约一半的节点。
  • 最坏情况：。当树退化成链表时，需遍历所有节点。

    // 2. 查找特定值的节点
    Node* search(Node* root, int key) {
        if (root == nullptr || root->data == key) return root;
        if (key < root->data) return search(root->left, key);
        return search(root->right, key);
    }

4.下一个最大节点

• 核心逻辑：这是指中序遍历中紧跟在当前节点后的节点。逻辑分为两类
  • 如果有右子树：最小值就在右子树的最左侧。
  • 如果没有右子树：需要向上回溯，直到找到一个节点，它是其父节点的左孩子。
• 时间复杂度：
  • 平均情况：。通常只需下行或上行几步。
  • 最坏情况：。在极端不平衡的树中，路径可能跨越整个树高。

    // 3. 查找下一个最大节点 (中序后继)
    Node* findSuccessor(Node* x) {
        if (x == nullptr) return nullptr;
    
        // 情况 A: 有右子树，后继是右子树的最小值
        if (x->right != nullptr) {
            return findMin(x->right);
        }
    
        // 情况 B: 无右子树，向上找第一个“左拐”的父节点
        Node* p = x->parent;
        while (p != nullptr && x == p->right) {
            x = p;
            p = p->parent;
        }
        return p;
    }

5.建立二叉搜索树

• 核心逻辑：建立 BST 的过程可以拆解为逐个元素的插入逻辑
  • 初始化：开始时树为空（root = nullptr）。
  • 比较与递归：
    • 如果树为空，创建一个新节点作为当前根节点。
    • 如果新值小于当前节点值，递归进入左子树。
    • 如果新值大于当前节点值，递归进入右子树。
    • （可选）如果新值等于当前节点值，通常根据需求选择忽略或插入到右子树。
  • 重复：对数组中的每一个元素重复上述过程。
• 时间复杂度：
  • 平均情况：
    当输入数据是随机分布时，树的高度趋于平衡（约 ）。插入 个节点，每个节点耗时 ，总计 。
  • 最好情况：
    当输入数据序列恰好能构造出一棵完全平衡的二叉树时，效率最高。
  • 最坏情况：
    如果输入数组是已经有序的，树会退化成一个单支链表。此时插入第 个节点需要 次比较，总时间复杂度为 。

// 插入单个节点的逻辑
Node* insert(Node* root, int val) {
    // 如果位置为空，在此处创建新节点
    if (root == nullptr) {
        return new Node(val);
    }

    // 递归寻找插入位置
    if (val < root->data) {
        root->left = insert(root->left, val);
    } else if (val > root->data) {
        root->right = insert(root->right, val);
    }
    // 注意：若 val == root->data，此处默认不处理（去重）

    return root;
}

// 建立整棵树的逻辑
Node* buildBST(const std::vector<int>& arr) {
    Node* root = nullptr;
    for (int x : arr) {
        root = insert(root, x);
    }
    return root;
}

6. 插入

插入逻辑：
基于 BST 的特性，插入的新节点始终作为叶子节点（避免破坏现有结构），步骤如下：

1. 空树处理：若 BST 为空，新节点直接作为根节点。
2. 遍历查找插入位置：
   • 从根节点开始，比较新节点值与当前节点值：
     • 若新值 < 当前节点值：向左子树遍历（若左子树为空，插入此处）。
     • 若新值 > 当前节点值：向右子树遍历（若右子树为空，插入此处）。
3. 插入节点：将新节点作为当前节点的左/右子节点。

代码实现：

// 二叉搜索树节点定义
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 递归版插入
TreeNode* insertRecursive(TreeNode* root, int val) {
    // 1. 空树：新节点作为根
    if (root == nullptr) {
        return new TreeNode(val);
    }
    // 2. 递归查找插入位置
    if (val < root->val) {
        root->left = insertRecursive(root->left, val); // 左子树插入
    } else if (val > root->val) {
        root->right = insertRecursive(root->right, val); // 右子树插入
    }
    // 3. 重复值：直接返回原节点（不处理）
    return root;
}

// 迭代版插入（空间效率更高，无递归栈开销）
TreeNode* insertIterative(TreeNode* root, int val) {
    TreeNode* newNode = new TreeNode(val);
    // 1. 空树：新节点作为根
    if (root == nullptr) {
        return newNode;
    }
    TreeNode* curr = root;
    TreeNode* parent = nullptr; // 记录当前节点的父节点
    // 2. 遍历查找插入位置
    while (curr != nullptr) {
        parent = curr;
        if (val < curr->val) {
            curr = curr->left;
        } else if (val > curr->val) {
            curr = curr->right;
        } else {
            // 重复值：释放新节点，返回原树
            delete newNode;
            return root;
        }
    }
    // 3. 插入新节点到父节点的左/右子树
    if (val < parent->val) {
        parent->left = newNode;
    } else {
        parent->right = newNode;
    }
    return root;
}

示例：
插入序列 [5, 3, 7, 2, 4, 6, 8]：

• 插入 5 → 根节点为 5；
• 插入 3 → 5 的左子节点；
• 插入 7 → 5 的右子节点；
• 插入 2 → 3 的左子节点；
• 插入 4 → 3 的右子节点；
• 最终 BST 结构：

      5
     / \
    3   7
   / \ / \
  2  4 6  8

7.删除

删除操作是 BST 中最复杂的操作，需保证删除后仍满足 BST 特性，关键是找到删除节点的“替代节点”，步骤如下：
设待删除节点为 target，其父节点为 parent：

1. 场景1：target 是叶子节点（无左、右子节点）

   • 直接删除：将 parent 指向 target 的指针设为 nullptr，释放 target。

2. 场景2：target 只有一个子节点（左子树或右子树非空）

   • 替代逻辑：用 target 的子节点替代 target 的位置（保持 BST 特性）。
   • 操作：若 target 是 parent 的左子节点，则 parent->left = target->子节点；若为右子节点，则 parent->right = target->子节点，释放 target。

3. 场景3：target 有两个子节点（左、右子树均非空）

   • 核心逻辑：不能直接删除，需找 target 的中序后继节点（右子树中最小的节点）或中序前驱节点（左子树中最大的节点）作为替代，步骤：
     1. 找到 target 的中序后继 successor（右子树一路向左到底的节点）；
     2. 用 successor 的值覆盖 target 的值；
     3. 删除 successor（successor 最多只有一个右子节点，属于场景1或场景2）。

代码实现：

// 辅助函数：找到以 root 为根的树的最小值节点（中序后继的核心）
TreeNode* findMin(TreeNode* root) {
    while (root->left != nullptr) {
        root = root->left;
    }
    return root;
}

// 递归版删除
TreeNode* deleteNode(TreeNode* root, int val) {
    if (root == nullptr) {
        return nullptr; // 未找到待删除节点，返回原树
    }

    // 1. 递归查找待删除节点
    if (val < root->val) {
        root->left = deleteNode(root->left, val); // 左子树查找删除
    } else if (val > root->val) {
        root->right = deleteNode(root->right, val); // 右子树查找删除
    } else {
        // 2. 找到待删除节点 root，处理三种场景
        // 场景1：叶子节点（无左、右子树）
        if (root->left == nullptr && root->right == nullptr) {
            delete root;
            return nullptr;
        }
        // 场景2：只有一个子节点（左空或右空）
        else if (root->left == nullptr) { // 只有右子节点
            TreeNode* temp = root->right;
            delete root;
            return temp; // 右子节点替代当前节点
        } else if (root->right == nullptr) { // 只有左子节点
            TreeNode* temp = root->left;
            delete root;
            return temp; // 左子节点替代当前节点
        }
        // 场景3：有两个子节点（找中序后继替代）
        else {
            // 找到中序后继（右子树最小值节点）
            TreeNode* successor = findMin(root->right);
            // 用后继节点的值覆盖当前节点
            root->val = successor->val;
            // 删除后继节点（递归处理，后继最多只有一个右子节点）
            root->right = deleteNode(root->right, successor->val);
        }
    }
    return root;
}

示例：
BST 结构如下，删除根节点 5（有两个子节点）：

    5
   / \
  3   7
 / \ / \
2  4 6  8

1. 找到 5 的中序后继：右子树（7）的最小值节点 6；
2. 用 6 的值覆盖 5 → 根节点变为 6；
3. 删除原后继节点 6（6 是叶子节点，场景1）；
4. 删除后 BST 结构：

       6
      / \
     3   7
    / \   \
   2  4   8

   中序遍历结果仍为升序：2→3→4→6→7→8，符合 BST 特性。

五、Huffman 编码树

1. 基本概念

• 定义： 一种带权路径长度最短的二叉树，也称为最优二叉树
• 带权路径长度 (WPL)：
  • : 第 个叶子节点的权重（通常是字符出现的频率）。
  • : 根节点到该叶子节点的路径长度（编码的位数）。
• 构造方法： 贪心算法。每次选择森林中权重最小的两个根节点，将它们合并为一个新的父节点，并将其权重设置为二者之和。重复直到只剩下一棵树。

2. 关键应用：Huffman 编码

• 目的： 是一种变长编码方法，用于数据压缩。
• 原理： 出现频率高的字符，赋予较短的编码（路径短）；出现频率低的字符，赋予较长的编码（路径长）。
• 特性： Huffman 编码是一种前缀编码，即任何字符的编码都不是另一个字符编码的前缀，这使得解码时不会产生歧义。

六、二叉树的存储表示

1. 链式存储 (Linked Representation): 每个节点包含数据域、左子节点指针和右子节点指针。这是最灵活的方式，支持所有操作。
2. 顺序存储 (Array Representation): 使用数组按层次顺序存储节点。
   • 要求： 通常用于完全二叉树。
   • 优点： 节省存储指针的空间，且可以快速定位父子节点（i从1开始）：
     • 节点 的父节点：
     • 节点 的左子节点：
     • 节点 的右子节点：
   • 缺点： 如果不是完全二叉树，会有大量空间浪费。

七.AVL

1. AVL 树的核心规则

• 平衡因子：每个节点都会记录其左子树高度与右子树高度的差值（）。
• 平衡条件：AVL 树要求所有节点的平衡因子的绝对值都不超过 1（即 ）。一旦某个节点的 ，就必须通过旋转来重新恢复平衡。
• 高度：AVL的高度为

2. 四种旋转操作

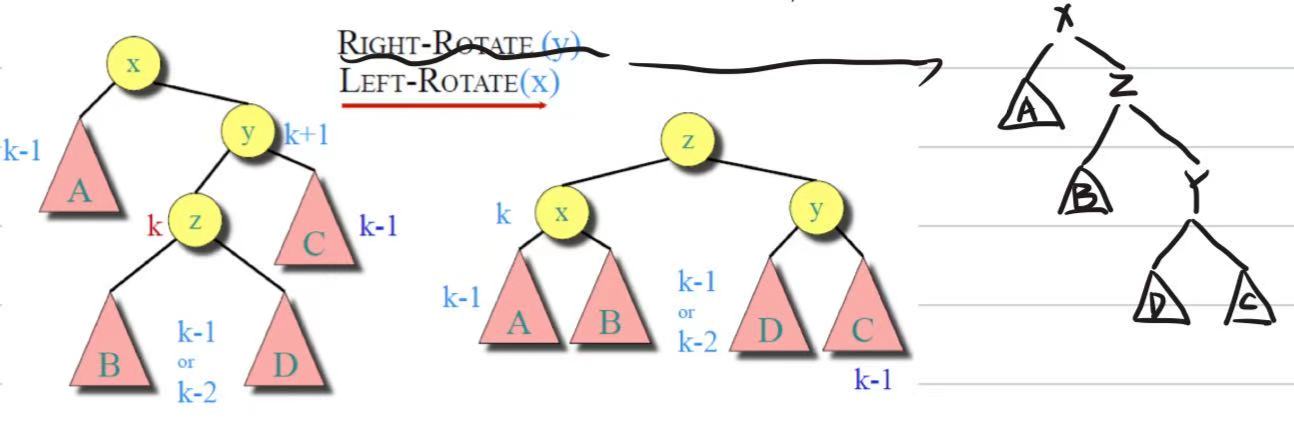
当插入新节点导致失衡时，根据新节点相对于失衡节点的位置，分为四种旋转场景：

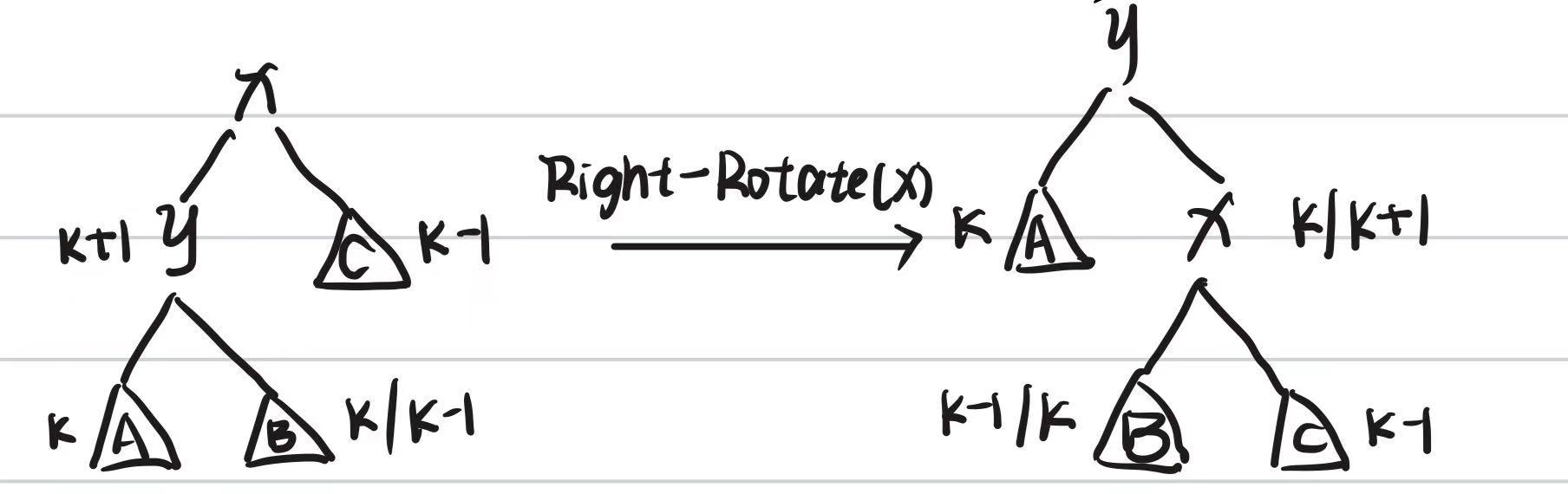
1. LL（左左型）：新节点插在左孩子的左子树。执行一次右旋。
   
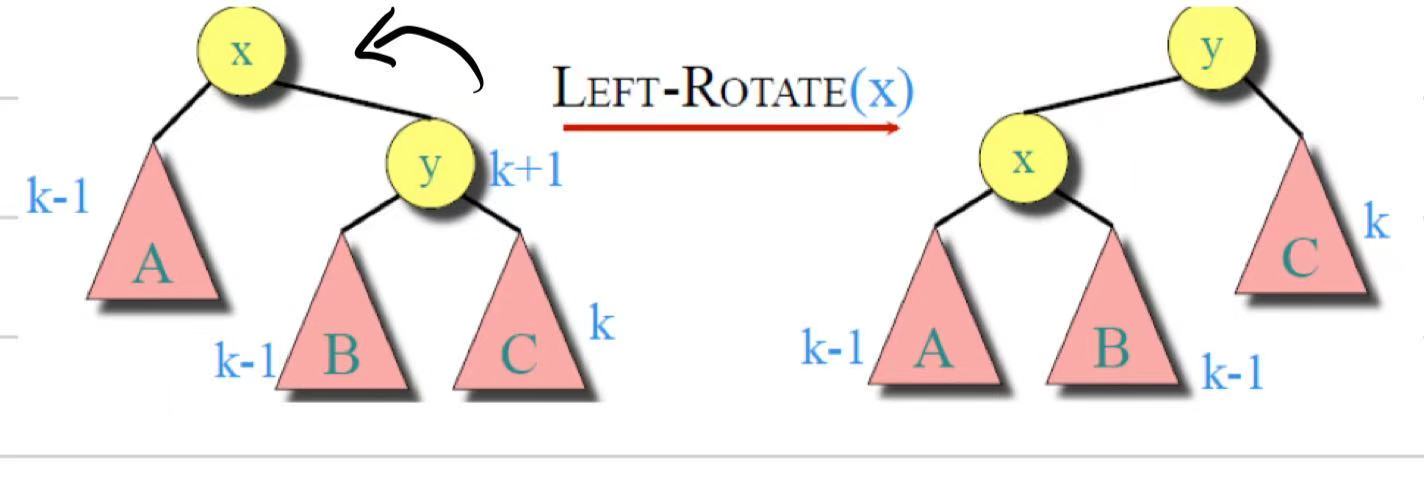
2. RR（右右型）：新节点插在右孩子的右子树。执行一次左旋。
   
   
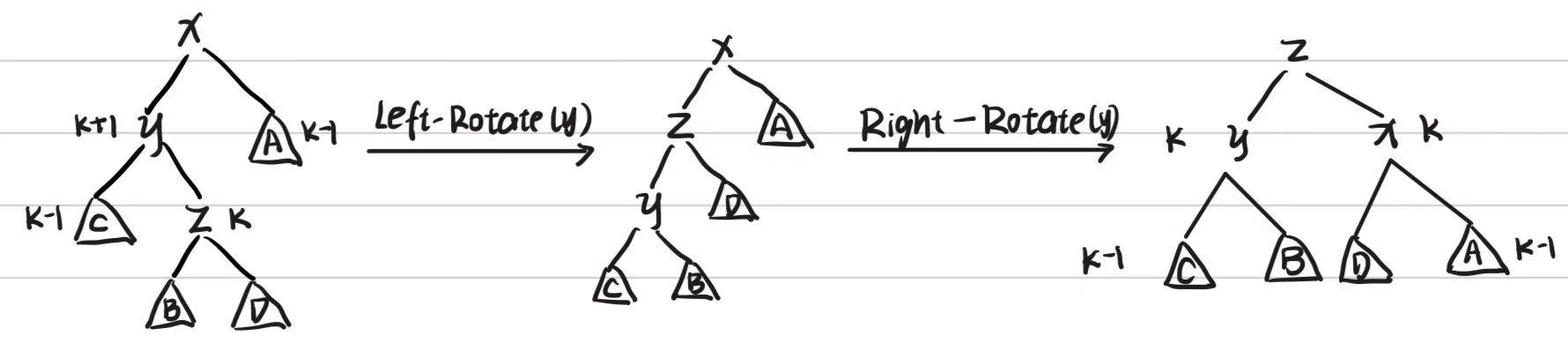
3. LR（左右型）：新节点插在左孩子的右子树。先对左孩子左旋，再对根节点右旋。
   
4. RL（右左型）：新节点插在右孩子的左子树。先对右孩子右旋，再对根节点左旋。