排序算法 | 宇宙尽头的森林

一、排序的基本概念

1. 什么是排序？

排序是将一个无序的序列按照某种既定规则（通常是元素的大小关系）重新排列成有序序列的过程。

例如：将数组 [3, 1, 4, 1, 5, 9] 按照升序排列为 [1, 1, 3, 4, 5, 9]。

2. 排序的核心要素

比较器：定义元素之间的“大小”关系。默认通常是 a < b（升序）或 a > b（降序）。
稳定性：
- 稳定排序：如果两个元素的值相等，它们在排序后的相对位置保持不变。
  - 例如：[(2, "a"), (1, "b"), (2, "c")] 稳定排序后可能是 [(1, "b"), (2, "a"), (2, "c")]。
- 不稳定排序：相等元素的相对位置可能发生变化。
  - 例如：上述例子不稳定排序后可能是 [(1, "b"), (2, "c"), (2, "a")]。
原地排序：排序过程中不使用额外的存储空间（或仅使用常数级的额外空间），直接修改原始序列。
时间复杂度：排序算法执行所需的时间与数据规模 n 的关系（通常关注最坏情况或平均情况）。
空间复杂度：排序算法执行所需的额外存储空间与数据规模 n 的关系。

二、常见排序算法分类

排序算法可以分为比较类排序和非比较类排序两大类：

1. 比较类排序

通过比较元素之间的大小来决定它们的相对位置。时间复杂度通常为 O(n^2) 或 O(n log n)。
常见算法：

插入排序
冒泡排序
选择排序
快速排序
归并排序
堆排序

2. 非比较类排序

不通过比较元素大小，而是利用元素本身的特性（如数字的位数、计数等）来排序。时间复杂度可以达到 O(n)，但适用场景有限。

常见算法：

计数排序（Counting Sort）
基数排序（Radix Sort）
桶排序（Bucket Sort）

三、常用排序算法详解

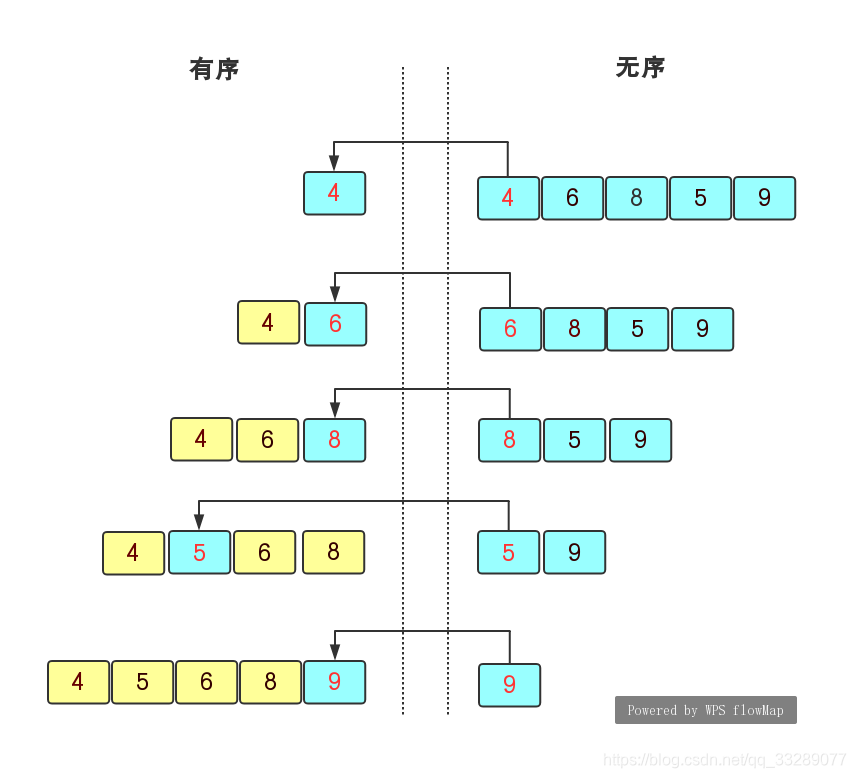
1. 插入排序

核心思想：将待排序元素逐个插入到已排序的子序列中，直到整个序列有序。
实现步骤：
1.从第一个元素开始，该元素可以认为已经被排序。
2.取出下一个元素，在已经排序的元素序列中从后向前扫描。
3.如果该元素（已排序）大于新元素，将该元素移到下一位置。
4.重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
5.将新元素插入到该位置后。
6.重复步骤2~5。
时间复杂度：
- 最好情况：。如果数组本身就是有序的，内层 while 循环几乎不执行。
- 最坏情况：。如果数组是完全倒序的，每次都要移动大量元素。
- 平均情况：。
空间复杂度：O(1)（原地排序）。
稳定性：稳定。
适用场景：小规模数据或接近有序的数据。

#include <iostream>
#include <vector>

// 插入排序函数
// arr: 待排序的向量
// ascending: true 表示升序，false 表示降序
void insertionSort(std::vector<int>& arr, bool ascending = true) {
    int n = arr.size();
    // 从第二个元素开始，逐个将元素插入到已排序的子序列中
    for (int i = 1; i < n; ++i) {
        int key = arr[i]; // 当前待插入的元素
        int j = i - 1;    // 已排序子序列的最后一个元素索引

        // 将比 key 大（或小）的元素向后移动
        if (ascending) {
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
        } else {
            while (j >= 0 && arr[j] < key) {
                arr[j + 1] = arr[j];
                j--;
            }
        }

        // 将 key 插入到正确的位置
        arr[j + 1] = key;
    }
}

int main() {
    std::vector<int> arr = {12, 11, 13, 5, 6};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    insertionSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    insertionSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

2. 冒泡排序

核心思想：重复遍历序列，每次比较相邻的两个元素，如果它们的顺序错误就交换位置，直到整个序列有序（较大的元素会像“气泡”一样浮到序列末尾）。
实现步骤：
1. 遍历序列，比较相邻元素，若前大后小则交换。
2. 每遍历一次，最大的元素会“冒泡”到末尾。
3. 重复步骤 1 和 2，直到没有元素需要交换。
时间复杂度：
- 最好情况：O(n)（序列已有序，加标志位优化）。
- 最坏情况：O(n^2)。
- 平均情况：O(n^2)。
空间复杂度：O(1)（原地排序）。
稳定性：稳定。

适用场景：小规模数据，或作为教学示例。

#include <iostream>
#include <vector>

// 冒泡排序函数
// arr: 待排序的向量
// ascending: true 表示升序，false 表示降序
void bubbleSort(std::vector<int>& arr, bool ascending = true) {
    int n = arr.size();
    bool swapped; // 标记是否发生了交换

    // 外层循环控制排序轮数
    for (int i = 0; i < n - 1; ++i) {
        swapped = false;
        // 内层循环进行相邻元素比较和交换
        // 每一轮结束后，最大（或最小）的元素会"冒泡"到末尾
        for (int j = 0; j < n - i - 1; ++j) {
            if (ascending) {
                if (arr[j] > arr[j + 1]) {
                    std::swap(arr[j], arr[j + 1]);
                    swapped = true;
                }
            } else {
                if (arr[j] < arr[j + 1]) {
                    std::swap(arr[j], arr[j + 1]);
                    swapped = true;
                }
            }
        }
        // 如果某一轮没有发生交换，说明数组已经有序，可以提前退出
        if (!swapped) {
            break;
        }
    }
}

int main() {
    std::vector<int> arr = {64, 34, 25, 12, 22, 11, 90};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    bubbleSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    bubbleSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

3. 选择排序

核心思想：每次从待排序序列中找到最小（或最大）的元素，将其与序列的起始位置交换，然后在剩余元素中重复此过程。
实现步骤：
1. 在待排序序列中找到最小元素的索引。
2. 将最小元素与序列的第一个元素交换。
3. 在剩余的元素中重复步骤 1 和 2，直到整个序列有序。
时间复杂度：
- 最好情况/最坏情况/平均情况：O(n^2)（无论序列是否有序，都需要遍历找最小元素）。
空间复杂度：O(1)（原地排序）。
稳定性：不稳定（例如 [2, 2, 1]，第一次选择会将 1 与第一个 2 交换，导致两个 2 的相对位置变化）。

适用场景：小规模数据，或对稳定性无要求的场景。

#include <iostream>
#include <vector>

// 选择排序函数
// arr: 待排序的向量
// ascending: true 表示升序，false 表示降序
void selectionSort(std::vector<int>& arr, bool ascending = true) {
    int n = arr.size();

    // 外层循环控制选择的轮数
    for (int i = 0; i < n - 1; ++i) {
        // 假设当前索引 i 是最小（或最大）元素的索引
        int target_idx = i;

        // 内层循环在未排序部分中找到最小（或最大）元素的索引
        for (int j = i + 1; j < n; ++j) {
            if (ascending) {
                if (arr[j] < arr[target_idx]) {
                    target_idx = j;
                }
            } else {
                if (arr[j] > arr[target_idx]) {
                    target_idx = j;
                }
            }
        }

        // 将找到的最小（或最大）元素与未排序部分的第一个元素交换
        if (target_idx != i) {
            std::swap(arr[i], arr[target_idx]);
        }
    }
}

int main() {
    std::vector<int> arr = {64, 25, 12, 22, 11};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    selectionSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    selectionSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

4. 快速排序

核心思想：“分治法”——选择一个“基准元素”，将序列分为两部分，一部分元素小于基准，另一部分大于基准，然后递归地对这两部分进行排序。
实现步骤：
1. 选择序列中的一个元素作为基准（通常是第一个、最后一个或中间元素）。
2. 遍历序列，将小于基准的元素放到基准左边，大于基准的元素放到右边（分区操作）。
3. 递归地对基准左边和右边的子序列进行快速排序。
时间复杂度：
- 最好情况/平均情况：O(n log n)。
- 最坏情况：O(n^2)（当序列已有序或逆序，且每次选择的基准是极值时）。
空间复杂度：O(log n)（递归栈空间，平均情况），最坏情况 O(n)。
稳定性：不稳定。

适用场景：大规模数据排序，是实践中最常用的排序算法之一（C++ std::sort 底层就是快速排序的变种）。

#include <iostream>
#include <vector>
#include <algorithm> // for std::swap

// 分区函数：将数组分区，并返回基准元素的最终位置
// [low, high] 是当前分区的范围
int partition(std::vector<int>& arr, int low, int high, bool ascending) {
    int pivot = arr[high]; // 选择最右边的元素作为基准
    int i = low - 1;       // i 是小于（或大于）基准区域的边界

    for (int j = low; j < high; ++j) {
        // 如果当前元素小于（或大于）等于基准，则将其加入相应区域
        if (ascending) {
            if (arr[j] <= pivot) {
                i++;
                std::swap(arr[i], arr[j]);
            }
        } else {
            if (arr[j] >= pivot) {
                i++;
                std::swap(arr[i], arr[j]);
            }
        }
    }
    // 将基准元素放到它的最终位置
    std::swap(arr[i + 1], arr[high]);
    return i + 1;
}

// 快速排序递归函数
void quickSortRecursive(std::vector<int>& arr, int low, int high, bool ascending) {
    if (low < high) {
        // pi 是分区后的基准元素索引
        int pi = partition(arr, low, high, ascending);

        // 递归地对基准元素左边和右边的子数组进行排序
        quickSortRecursive(arr, low, pi - 1, ascending);
        quickSortRecursive(arr, pi + 1, high, ascending);
    }
}

// 快速排序入口函数
void quickSort(std::vector<int>& arr, bool ascending = true) {
    if (arr.empty()) return;
    quickSortRecursive(arr, 0, arr.size() - 1, ascending);
}

int main() {
    std::vector<int> arr = {10, 7, 8, 9, 1, 5};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    quickSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    quickSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

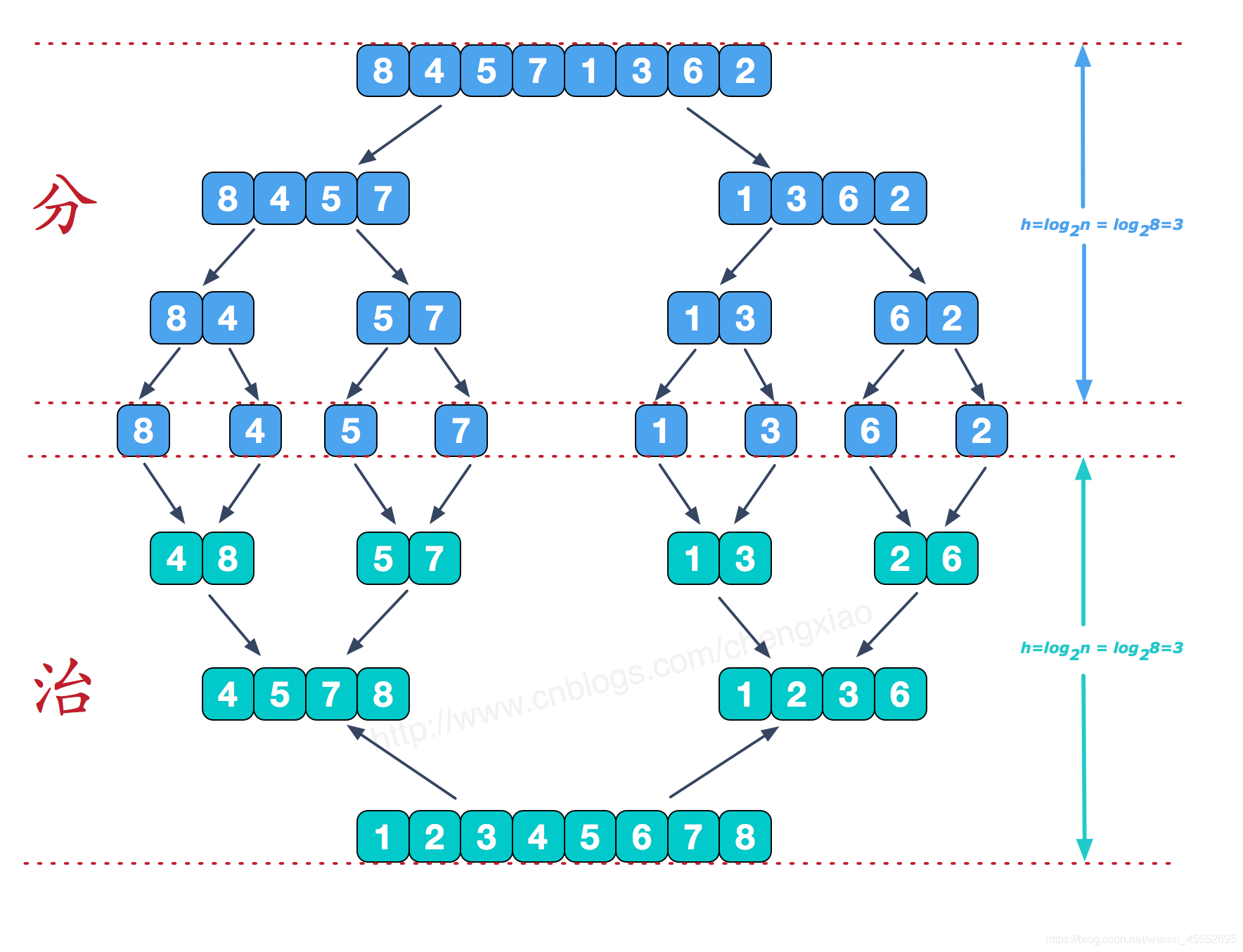
5. 归并排序

核心思想：
- 分解：将当前序列不断从中间切分，直到每个子序列只剩下一个元素（一个元素天然是有序的）。
- 合并：将两个有序的小序列合并成一个更大的有序序列，直到最终合并为完整的排序数组。
  - 在合并两个有序数组 L 和 R 时，我们使用两个指针分别指向它们的开头，比较指向的元素，将较小者放入临时数组中，然后移动指针。重复此过程直到所有元素都被放入临时数组。
实现步骤：
1. 如果序列长度为 1，则已经有序，直接返回。
2. 将序列分成左右两个子序列，递归地对它们进行归并排序。
3. 将两个有序的子序列合并成一个有序序列（合并操作）。
时间复杂度：
- 最好情况/最坏情况/平均情况：O(n log n)。
- 无论初始状态如何，数组总是被划分为层，每层合并的操作量都是。
空间复杂度：O(n)
- 归并排序需要一个与原数组等大的辅助空间来存放临时合并的结果，这也是它相对于快速排序（原地排序）的一个劣势。
稳定性：稳定。
适用场景：大规模数据排序，尤其是对稳定性有要求的场景（例如 std::stable_sort 底层通常是归并排序）。

#include <iostream>
#include <vector>

// 合并函数：将两个有序子数组合并成一个有序数组
// arr: 原始数组
// left, mid, right: 左、中、右边界
// temp: 临时数组，用于存储合并结果
void merge(std::vector<int>& arr, int left, int mid, int right, bool ascending, std::vector<int>& temp) {
    int i = left;   // 左子数组的起始索引
    int j = mid + 1;// 右子数组的起始索引
    int k = left;   // 临时数组的起始索引

    // 比较两个子数组的元素，将较小（或较大）的元素放入临时数组
    while (i <= mid && j <= right) {
        if (ascending) {
            if (arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        } else {
            if (arr[i] >= arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
    }

    // 将左子数组中剩余的元素复制到临时数组
    while (i <= mid) {
        temp[k++] = arr[i++];
    }

    // 将右子数组中剩余的元素复制到临时数组
    while (j <= right) {
        temp[k++] = arr[j++];
    }

    // 将临时数组中的结果复制回原始数组
    for (int x = left; x <= right; ++x) {
        arr[x] = temp[x];
    }
}

// 归并排序递归函数
void mergeSortRecursive(std::vector<int>& arr, int left, int right, bool ascending, std::vector<int>& temp) {
    if (left < right) {
        int mid = left + (right - left) / 2; // 计算中间点，避免溢出

        // 递归地对左右两个子数组进行排序
        mergeSortRecursive(arr, left, mid, ascending, temp);
        mergeSortRecursive(arr, mid + 1, right, ascending, temp);

        // 合并两个已排序的子数组
        merge(arr, left, mid, right, ascending, temp);
    }
}

// 归并排序入口函数
void mergeSort(std::vector<int>& arr, bool ascending = true) {
    if (arr.empty()) return;
    std::vector<int> temp(arr.size()); // 创建一个与原数组大小相同的临时数组
    mergeSortRecursive(arr, 0, arr.size() - 1, ascending, temp);
}

int main() {
    std::vector<int> arr = {12, 11, 13, 5, 6, 7};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    mergeSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    mergeSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

6. 堆排序

核心思想：利用“堆”这种数据结构的特性（堆顶元素是最大或最小元素），每次取出堆顶元素，然后调整堆，重复此过程直到堆为空。

实现步骤：

1. 将待排序序列构建成一个大顶堆（或小顶堆）。
2. 将堆顶元素（最大或最小）与堆的最后一个元素交换。
3. 调整堆的大小（减少 1），并对新的堆顶元素进行“下沉”操作，维持堆的性质。
4. 重复步骤 2 和 3，直到堆为空。

时间复杂度：
- 最好、最坏、平均：均为。
- 建堆的时间复杂度为，随后进行次调整，每次调整。
空间复杂度：。
- 直接在原数组上操作，不需要额外空间，这是它优于归并排序的地方。
稳定性：不稳定。
- 由于在交换堆顶和末尾元素时，可能会破坏相等元素的相对顺序。

适用场景：大规模数据排序，对空间复杂度要求较高的场景。

#include <iostream>
#include <vector>
#include <algorithm> // for std::swap

// 堆调整函数（大顶堆）
// arr: 待调整的数组
// size: 堆的大小
// i: 当前需要调整的节点索引
void heapifyMax(std::vector<int>& arr, int size, int i) {
    int largest = i;       // 初始化最大元素为根节点
    int left = 2 * i + 1;  // 左子节点索引
    int right = 2 * i + 2; // 右子节点索引

    // 如果左子节点大于根节点
    if (left < size && arr[left] > arr[largest]) {
        largest = left;
    }

    // 如果右子节点大于当前最大元素
    if (right < size && arr[right] > arr[largest]) {
        largest = right;
    }

    // 如果最大元素不是根节点
    if (largest != i) {
        std::swap(arr[i], arr[largest]);

        // 递归地调整受影响的子树
        heapifyMax(arr, size, largest);
    }
}

// 堆调整函数（小顶堆）
void heapifyMin(std::vector<int>& arr, int size, int i) {
    int smallest = i;      // 初始化最小元素为根节点
    int left = 2 * i + 1;  // 左子节点索引
    int right = 2 * i + 2; // 右子节点索引

    if (left < size && arr[left] < arr[smallest]) {
        smallest = left;
    }

    if (right < size && arr[right] < arr[smallest]) {
        smallest = right;
    }

    if (smallest != i) {
        std::swap(arr[i], arr[smallest]);
        heapifyMin(arr, size, smallest);
    }
}

// 堆排序函数
// arr: 待排序的数组
// ascending: true 表示升序，false 表示降序
void heapSort(std::vector<int>& arr, bool ascending = true) {
    int n = arr.size();

    // 1. 构建堆
    // 从最后一个非叶子节点开始向上调整
    if (ascending) {
        // 构建大顶堆用于升序排序
        for (int i = n / 2 - 1; i >= 0; --i) {
            heapifyMax(arr, n, i);
        }
    } else {
        // 构建小顶堆用于降序排序
        for (int i = n / 2 - 1; i >= 0; --i) {
            heapifyMin(arr, n, i);
        }
    }

    // 2. 从堆中提取元素
    for (int i = n - 1; i > 0; --i) {
        // 将堆顶元素（最大或最小）与当前堆的最后一个元素交换
        std::swap(arr[0], arr[i]);

        // 调整剩余的元素，维持堆的性质
        if (ascending) {
            heapifyMax(arr, i, 0);
        } else {
            heapifyMin(arr, i, 0);
        }
    }
}

int main() {
    std::vector<int> arr = {12, 11, 13, 5, 6, 7};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    heapSort(arr); // 默认升序排序
    
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    heapSort(arr, false); // 降序排序
    
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

7.基于二叉搜索树的排序

核心流程：
- 构建 BST：遍历待排序数组，将每个元素逐个插入到一棵二叉搜索树中。
  - 根据 BST 的性质：左子树的所有节点 < 根节点 < 右子树的所有节点。
- 中序遍历：对构建好的二叉搜索树进行中序遍历。
  - 按照“左子树根节点右子树”的顺序读取，得到的序列自然就是有序的。
时间复杂度
- 在平均/最好情况下，BST Sort 的表现为。
- 在最坏情况下（例如输入数据已经是有序的），BST 会退化成一条直线（链表），此时性能会大幅下降至。
空间复杂度：O(n)
稳定性：稳定

#include <iostream>
#include <vector>

using namespace std;

// BST 节点结构
struct Node {
    int key;
    Node *left, *right;
    Node(int item) : key(item), left(nullptr), right(nullptr) {}
};

// 将新值插入 BST
Node* insert(Node* node, int key) {
    if (node == nullptr) return new Node(key);

    if (key < node->key)
        node->left = insert(node->left, key);
    else
        node->right = insert(node->right, key);

    return node;
}

// 中序遍历并将结果存回数组
void storeSorted(Node* root, vector<int>& arr, int& i) {
    if (root != nullptr) {
        storeSorted(root->left, arr, i);
        arr[i++] = root->key;
        storeSorted(root->right, arr, i);
    }
}

// BST 排序主函数
void treeSort(vector<int>& arr) {
    Node* root = nullptr;

    // 1. 构建 BST
    for (int x : arr) {
        root = insert(root, x);
    }

    // 2. 中序遍历回填数组
    int i = 0;
    storeSorted(root, arr, i);
}

int main() {
    vector<int> arr = {5, 4, 7, 2, 11};
    treeSort(arr);

    for (int x : arr) cout << x << " "; // 输出: 2 4 5 7 11
    return 0;
}

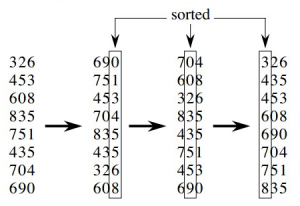
8.基数排序

核心原理：将整数按位数切割成不同的数字，然后按每个位数分别比较。
- 第一步：先按所有数字的个位进行排序，放入 0-9 号“桶”中。
- 第二步：保持个位的相对顺序，再按十位进行排序。
- 第三步：保持前两步的相对顺序，最后按百位进行排序。
时间复杂度：
- **
- 其中是元素个数，是数字的最大位数（如三位数），是基数范围（十进制中）。由于和对于特定类型通常是常数，基数排序在处理大量整数时往往比的算法更快。
空间复杂度：
- **
- 需要额外的 output 数组和 count 桶空间。
稳定性：
- 稳定。基数排序必须依赖稳定的子排序过程（如计数排序），否则高位的排序会打乱低位已排好的顺序。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 获取数组中的最大值，以确定需要排序多少位
int getMax(const vector<int>& arr) {
    int maxVal = arr[0];
    for (int x : arr) if (x > maxVal) maxVal = x;
    return maxVal;
}

// 对数组按照指定的位（exp，如1, 10, 100）进行计数排序
void countingSortByDigit(vector<int>& arr, int exp) {
    int n = arr.size();
    vector<int> output(n); // 输出数组
    int count[10] = {0};   // 桶，存放0-9出现的次数

    // 统计每个数字出现的次数
    for (int i = 0; i < n; i++) {
        count[(arr[i] / exp) % 10]++;
    }

    // 将 count 转换为前缀和，确定数字在输出数组中的位置
    for (int i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    // 反向填充 output 数组，保证排序的稳定性
    for (int i = n - 1; i >= 0; i--) {
        int digit = (arr[i] / exp) % 10;
        output[count[digit] - 1] = arr[i];
        count[digit]--;
    }

    // 将排序好的数据复制回原数组
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }
}

// 基数排序主函数
void radixSort(vector<int>& arr) {
    if (arr.empty()) return;

    // 找到最大数
    int m = getMax(arr);

    // 从个位开始，对每一位进行计数排序
    // exp 为 1, 10, 100, ...
    for (int exp = 1; m / exp > 0; exp *= 10) {
        countingSortByDigit(arr, exp);
    }
}

void printArray(const vector<int>& arr) {
    for (int x : arr) cout << x << " ";
    cout << endl;
}

int main() {
    vector<int> arr = {170, 45, 75, 90, 802, 24, 2, 66};
    cout << "原数组: ";
    printArray(arr);

    radixSort(arr);

    cout << "排序后: ";
    printArray(arr);
    return 0;
}

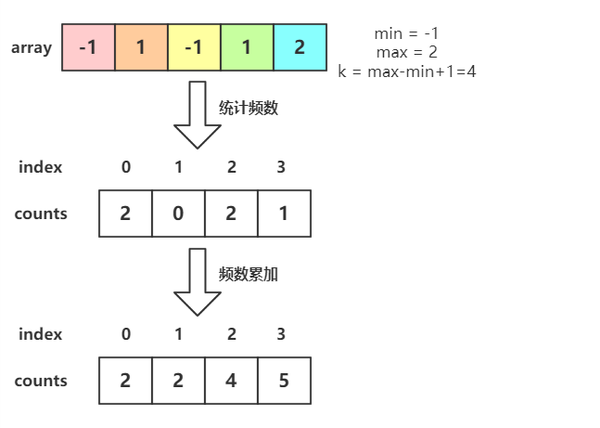
9. 计数排序

核心思想：
- 非比较排序：计数排序不通过元素间的比较来决定顺序，而是利用数组下标来确定元素的正确位置。
- 空间换时间：通过统计每个元素出现的次数，直接计算出每个元素在输出序列中的位置。它要求输入数据必须是有确定范围的整数

实现步骤：

1. 找范围：找出待排序数组中最大和最小的元素，确定统计数组（桶）的大小。
2. 统计次数：遍历原数组，在统计数组中记录每个元素出现的频率。
3. 累加计数：对统计数组进行前缀和运算，使得`count[i]` 存储的是小于等于 i 的元素总个数。
4. 反向填充：反向遍历原数组，根据统计数组中的位置信息将元素放入结果数组，并递减统计数组中的计数值（反向遍历是为了保证排序的稳定性）。

时间复杂度：
- 最好情况/最坏情况/平均情况：。
- 其中为元素个数，为数据的取值范围（）。当时，复杂度为线性。
空间复杂度：
- 需要一个大小为的统计数组和一个大小为的结果数组。
稳定性：稳定。
- 在反向填充步骤中，相同元素的相对顺序被保留。

适用场景：适用于数据范围

远小于

的整数排序（如统计考试分数、年龄分布等）。

#include <iostream>
#include <vector>
#include <algorithm>

// 计数排序函数
// arr: 原始数组
// ascending: 是否升序
void countingSort(std::vector<int>& arr, bool ascending = true) {
    if (arr.empty()) return;

    // 1. 寻找最大值和最小值以确定范围
    int maxVal = *std::max_element(arr.begin(), arr.end());
    int minVal = *std::min_element(arr.begin(), arr.end());
    int range = maxVal - minVal + 1;

    // 2. 统计每个元素出现的次数
    std::vector<int> count(range, 0);
    for (int x : arr) {
        count[x - minVal]++;
    }

    // 3. 累加计数（计算前缀和），确定每个元素的最后位置
    if (ascending) {
        for (int i = 1; i < range; ++i) {
            count[i] += count[i - 1];
        }
    } else {
        // 如果是降序，则从后往前累加
        for (int i = range - 2; i >= 0; --i) {
            count[i] += count[i + 1];
        }
    }

    // 4. 反向遍历原数组，保证稳定性，填充结果数组
    std::vector<int> output(arr.size());
    for (int i = arr.size() - 1; i >= 0; --i) {
        int val = arr[i];
        int pos = count[val - minVal] - 1; // 获取在输出数组中的索引
        output[pos] = val;
        count[val - minVal]--; // 更新位置，供下一个相同元素使用
    }

    // 将结果复制回原数组
    arr = output;
}

int main() {
    std::vector<int> arr = {4, 2, 2, 8, 3, 3, 1};
    
    std::cout << "Original array: ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    countingSort(arr, true); // 升序
    std::cout << "Sorted array (ascending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    countingSort(arr, false); // 降序
    std::cout << "Sorted array (descending): ";
    for (int x : arr) std::cout << x << " ";
    std::cout << std::endl;

    return 0;
}

四、排序算法性能对比

算法	时间复杂度（最坏）	时间复杂度（平均）	时间复杂度（最好）	空间复杂度	稳定性	原地排序
插入排序	`O(n^2)`	`O(n^2)`	`O(n)`	`O(1)`	稳定	是
冒泡排序	`O(n^2)`	`O(n^2)`	`O(n)`	`O(1)`	稳定	是
选择排序	`O(n^2)`	`O(n^2)`	`O(n^2)`	`O(1)`	不稳定	是
快速排序	`O(n^2)`	`O(n log n)`	`O(n log n)`	`O(log n)`	不稳定	是
归并排序	`O(n log n)`	`O(n log n)`	`O(n log n)`	`O(n)`	稳定	否
堆排序	`O(n log n)`	`O(n log n)`	`O(n log n)`	`O(1)`	不稳定	是
计数排序	`O(n + k)`	`O(n + k)`	`O(n + k)`	`O(k)`	稳定	否
基数排序	`O(d * (n + k))`	`O(d * (n + k))`	`O(d * (n + k))`	`O(n + k)`	稳定	否

说明：

k：计数排序中表示数据的范围，基数排序中表示每个位数的取值范围（通常为 10）。
d：基数排序中表示数据的最大位数。